点P到x轴的距离比它到点(0,1)的距离小1,称点P的轨迹为曲线C,点M为直线l:y=-m (m>0)上任意一点,过点M作曲线C的两条切线MA,MB,切点分别为A,B.
(1)求曲线C的轨迹方程;
(2)当M的坐标为(0,-l)时,求过M,A,B三点的圆的标准方程,并判断直线l与此圆的位置关系;
(3)当m变化时,试探究直线l上是否存在点M,使MA⊥MB?若存在,有几个这样的点,若不存在,请说明理由.
解:(1)∵点P到x轴的距离比点P到点(0,1)的距离小1,
∴点P到直线y=-1的距离等于点P到点(0,1)的距离,
∴点P的轨迹是焦点在(0,1),准线为y=-1的抛物线,
∴点P的轨迹方程为:x
2=4y.
(2)当M的坐标为(0,-1)时,设过M点的切线方程为y=kx-1,
代入x
2=4y,整理得x
2-4kx+4=0,①
令△=(4k)
2-4×4=0,解得k=±1,代入方程①得x=±2,故得A(2,1),B(-2,1),|AB|=4.
∵M到AB的中点(0,1)的距离为2,
∴过M,A,B三点的圆的标准方程为x
2+(y-1)
2=4.
易知圆与直线l:y=-1相切.
(3)设M(x
0,-m),过M的切线方程为:y=k(x-x
0)-m.
联立
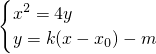
整理得 x
2-4kx+4(kx
0+m)=0,
∵直线与抛物线相切,∴△=0.
即16k
2-16(kx
0+m)=0,整理得k
2-kx
0-m=0,
∴k
MA+k
MB=x
0,k
MA•k
MB=-m
若MA⊥MB,则k
MA•k
MB=-m=-1.
即m=1时,直线l上任意一点M均有MA⊥MB;
m≠1时,MA与MB不垂直.
综上所述,当m=1时,直线l上存在无穷多个点M,使MA⊥MB,
当m≠1时,直线l上不存在满足条件的点M.
分析:(1)利用抛物线的定义即可得出其轨迹;
(2)当M的坐标为(0,-1)时,设过M点的切线方程为y=kx-1,与抛物线的方程联立,因为相切,可得△=0,即可解出斜率k,可得出点A,B的坐标,进而得到过三点A、B、M的圆的标准方程,即可判断出直线l与此圆的位置关系;
(3)设M(x
0,-m),过M的切线方程为:y=k(x-x
0)-m.与抛物线的方程联立,由于相切可得△=0,即可得到直线MA,MB的斜率满足的关系式,再利用垂直满足的关系式即可判断出答案.
点评:熟练掌握抛物线的定义、直线与抛物线相切转化为关于一个未知数的一元二次方程的△=0、根与系数的关系、直线相互垂直与斜率的关系、分类讨论的思想方法等是解题的关键.

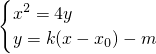 整理得 x2-4kx+4(kx0+m)=0,
整理得 x2-4kx+4(kx0+m)=0,
