
【题目】已知平面内两个定点![]() 和点
和点![]() ,
,![]() 是动点,且直线
是动点,且直线![]() ,
,![]() 的斜率乘积为常数
的斜率乘积为常数![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() .
.
① 存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离之和为定值;
距离之和为定值;
② 存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离之和为定值;
距离之和为定值;
③ 不存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离差的绝对值为定值;
距离差的绝对值为定值;
④ 不存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离差的绝对值为定值.
距离差的绝对值为定值.
其中正确的命题是_______________.(填出所有正确命题的序号)
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】某中学高一期中考试结束后,从高一年级1000名学生中任意抽取50名学生,将这50名学生的某一科的考试成绩(满分150分)作为样本进行统计,并作出样本成绩的频率分布直方图(如图).
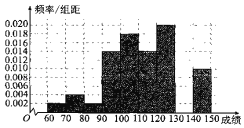
(1)由于工作疏忽,将成绩[130,140)的数据丢失,求此区间的人数及频率分布直方图的中位数;(结果保留两位小数)
(2)若规定考试分数不小于120分为优秀,现从样本的优秀学生中任意选出3名学生,参加学习经验交流会.设X表示参加学习经验交流会的学生分数不小于130分的学生人数,求X的分布列及期望;
(3)视样本频率为概率.由于特殊原因,有一个学生不能到学校参加考试,根据以往考试成绩,一般这名学生的成绩应在平均分左右.试根据以上数据,说明他若参加考试,可能得多少分?(每组数据以区问的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“伟大的变革—庆祝改革开放![]() 周年大型展览”于
周年大型展览”于![]() 年
年![]() 月
月![]() 日在中国国家博物馆闭幕,本次特展紧扣“改革开放
日在中国国家博物馆闭幕,本次特展紧扣“改革开放![]() 年光辉历程”的主线,多角度、全景式描绘了我国改革开放
年光辉历程”的主线,多角度、全景式描绘了我国改革开放![]() 年波澜壮阔的历史画卷.据统计,展览全程呈现出持续火爆的状态,现场观众累计达
年波澜壮阔的历史画卷.据统计,展览全程呈现出持续火爆的状态,现场观众累计达![]() 万人次,参展人数屡次创造国家博物馆参观纪录,网上展馆点击浏览总量达
万人次,参展人数屡次创造国家博物馆参观纪录,网上展馆点击浏览总量达![]() 亿次.
亿次.
下表是![]() 年
年![]() 月参观人数(单位:万人)统计表
月参观人数(单位:万人)统计表
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
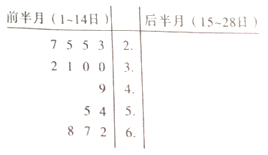
根据表中数据回答下列问题:
(1)请将![]() 年
年![]() 月前半月(
月前半月(![]() 日)和后半月(
日)和后半月(![]() 日)参观人数统计对比茎叶图填补完整,并通过茎叶图比较两组数据方差的大小(不要求计算出具体值,得出结论即可);
日)参观人数统计对比茎叶图填补完整,并通过茎叶图比较两组数据方差的大小(不要求计算出具体值,得出结论即可);
(2)将![]() 年
年![]() 月参观人数数据用该天的对应日期作为样本编号,现从中抽样
月参观人数数据用该天的对应日期作为样本编号,现从中抽样![]() 天的样本数据.若抽取的样本编号是以
天的样本数据.若抽取的样本编号是以![]() 为公差的等差数列,且数列的第
为公差的等差数列,且数列的第![]() 项为
项为![]() ,求抽出的这
,求抽出的这![]() 个样本数据的平均值;
个样本数据的平均值;
(3)根据国博以往展览数据及调查统计信息可知,单日入馆参观人数为![]() (含
(含![]() ,单位:万人)时,参观者的体验满意度最佳,在从
,单位:万人)时,参观者的体验满意度最佳,在从![]() 中抽出的样本数据中随机抽取三天的数据,参观者的体验满意度为最佳的天数记为
中抽出的样本数据中随机抽取三天的数据,参观者的体验满意度为最佳的天数记为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体![]() 中,E,F分别为线段CD和
中,E,F分别为线段CD和![]() 上的动点,且满足
上的动点,且满足![]() ,则四边形
,则四边形![]() 所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和( )
所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和( )

A. 有最小值![]() B. 有最大值
B. 有最大值![]() C. 为定值3D. 为定值2
C. 为定值3D. 为定值2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别是
)的左、右焦点分别是![]() ,
,![]() ,点
,点![]() 为
为![]() 的上顶点,点
的上顶点,点![]() 在
在![]() 上,
上,![]() ,且
,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,垂直于
两点,垂直于![]() 的直线
的直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区的区人大代表有教师6人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为![]() ,乙校教师记为
,乙校教师记为![]() ,丙校教师记为
,丙校教师记为![]() ,丁校教师记为
,丁校教师记为![]() .现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
.现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
(1)请列出十九大报告宣讲团组成人员的全部可能结果;
(2)求教师![]() 被选中的概率;
被选中的概率;
(3)求宣讲团中没有乙校教师代表的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某林场现有木材存量为![]() ,每年以25%的增长率逐年递增,但每年年底要砍伐的木材量为
,每年以25%的增长率逐年递增,但每年年底要砍伐的木材量为![]() ,经过
,经过![]() 年后林场木材存有量为
年后林场木材存有量为![]()
(1)求![]() 的解析式
的解析式
(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量不应少于![]() ,如果
,如果![]() ,那么该地区会发生水土流失吗?若会,要经过几年?(取
,那么该地区会发生水土流失吗?若会,要经过几年?(取![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com