
【题目】(本小题满分14分)已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若存在两条直线![]() ,
,![]() 都是曲线
都是曲线![]() 的切线,求实数
的切线,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;.(Ⅲ)
;.(Ⅲ)![]()
【解析】
试题分析:(Ⅰ)![]() ,对a进行分类讨论:当
,对a进行分类讨论:当![]() 时,
时,![]() ,则函数
,则函数![]() 的单调递减区间是
的单调递减区间是![]() .当
.当![]() 时,令
时,令![]() ,得
,得![]() .
.![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(Ⅱ)因为 存在两条直线
;(Ⅱ)因为 存在两条直线![]() ,
,![]() 都是曲线
都是曲线![]() 的切线,
的切线,
所以 ![]() 至少有两个不等的正实根,令
至少有两个不等的正实根,令![]() 得
得![]() ,记其两个实根分别为
,记其两个实根分别为![]() .
.
则 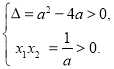 解得
解得![]() .再说明当
.再说明当![]() 时,曲线
时,曲线![]() 在点
在点![]() 处的切线分别为
处的切线分别为![]() ,
,![]() 是两条不同的直线即可;(Ⅲ)只需分类讨论.
是两条不同的直线即可;(Ⅲ)只需分类讨论.
试题解析:(Ⅰ)![]() . 1分
. 1分
当![]() 时,
时,![]() ,则函数
,则函数![]() 的单调递减区间是
的单调递减区间是![]() . 2分
. 2分
当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ |
所以 ![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() . 4分
. 4分
(Ⅱ)因为 存在两条直线![]() ,
,![]() 都是曲线
都是曲线![]() 的切线,
的切线,
所以 ![]() 至少有两个不等的正实根. 5分
至少有两个不等的正实根. 5分
令![]() 得
得![]() ,记其两个实根分别为
,记其两个实根分别为![]() .
.
则 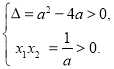 解得
解得![]() . 7分
. 7分
当![]() 时,曲线
时,曲线![]() 在点
在点![]() 处的切线分别为
处的切线分别为![]() ,
,![]() .
.
令![]() .
.
由![]() 得
得![]() (不妨设
(不妨设![]() ),且当
),且当![]() 时,
时,![]() 在
在![]() 上是单调函数.
上是单调函数.
所以 ![]() .
.
所以 ![]() ,
,![]() 是曲线
是曲线![]() 的两条不同的切线.
的两条不同的切线.
所以 实数![]() 的取值范围为
的取值范围为![]() . 9分
. 9分
(Ⅲ)当![]() 时,函数
时,函数![]() 是
是![]() 内的减函数.
内的减函数.
因为 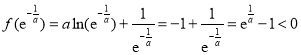 ,
,
而![]() ,不符合题意. 11分
,不符合题意. 11分
当![]() 时,由(Ⅰ)知:
时,由(Ⅰ)知:![]() 的最小值是
的最小值是![]() .
.
(ⅰ)若![]() ,即
,即![]() 时,
时,![]() ,
,
所以,![]() 符合题意.
符合题意.
(ⅱ)若![]() ,即
,即![]() 时,
时,![]() .
.
所以,![]() 符合题意.
符合题意.
(ⅲ)若![]() ,即
,即![]() 时,有
时,有![]() .
.
因为 ![]() ,函数
,函数![]() 在
在![]() 内是增函数,
内是增函数,
所以 当![]() 时,
时,![]() .
.
又因为 函数![]() 的定义域为
的定义域为![]() ,
,
所以 ![]() .
.
所以 ![]() 符合题意.
符合题意.
综上所述,实数![]() 的取值范围为
的取值范围为![]() . 14分
. 14分


科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的导数y′=f′(x)仍是x的函数,就把y′=f′(x)的导数y″=f″(x)叫做函数y=f(x)二阶导数,记做y(2)=f(2)(x).同样函数y=f(x)的n﹣1阶导数的导数叫做y=f(x)的n阶导数,表示y(n)=f(n)(x).在求y=ln(x+1)的n阶导数时,已求得 ![]() ,
, ![]() ,根据以上推理,函数y=ln(x+1)的第n阶导数为 .
,根据以上推理,函数y=ln(x+1)的第n阶导数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式: (x2+x+1)0=1
(x2+x+1)1=x2+x+1
(x2+x+1)2=x4+2x3+3x2+2x+1
(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1
…
观察多项式系数之间的关系,可以仿照杨辉三角构造如图所示的广义杨辉三角形,其构造方法为:第0行为1,以下各行每个数是它头上与左右两肩上3数(不足3数的,缺少的数计为0)之和,第k行共有2k+1个数.若在(1+ax)(x2+x+1)5的展开式中,x8项的系数为67,则实数a值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式(1﹣a)x2﹣4x+6>0的解集是{x|﹣3<x<1}.
(1)解不等式2x2+(2﹣a)x﹣a>0
(2)b为何值时,ax2+bx+3≥0的解集为R.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(2x+1)﹣ ![]() .
.
(1)证明:对任意的b∈R,函数f(x)=log2(2x+1)﹣ ![]() 的图象与直线y=
的图象与直线y= ![]() +b最多有一个交点;
+b最多有一个交点;
(2)设函数g(x)=log4(a﹣2x),若函数y=f(x)与函数y=g(x)的图象至少有一个交点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列f(x1),f(x2),…f(xn),…是公差为2的等差数列,且x1=a2其中函数f(x)=logax(a为常数且a>0,a≠1).
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)若an=logaxn , 求证 ![]() +
+ ![]() +…+
+…+ ![]() <1.
<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2x﹣ ![]() sinxcosx+1.
sinxcosx+1.
(1)求函数f(x)的单调递增区间;
(2)若f(θ)= ![]() ,θ∈(
,θ∈( ![]() ,
, ![]() ),求sin2θ的值.
),求sin2θ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com