
���� ��1����ϴ˷�Χ����֤����ȷ�ԣ�
��2��һ�����Ϊ����n��N*����$\sqrt{n}+\sqrt{n+2}��2\sqrt{n+1}$���÷��������ۺϷ�����֤����
��� �⣺��1����֤��ʽ��������$\sqrt{3}��1.74$��
��$\sqrt{1}+\sqrt{3}��2.74$��
��$\sqrt{2}��1.41$��
��$2\sqrt{2}��2.82$��
��$\sqrt{1}+\sqrt{3}��2\sqrt{2}$
��2��һ�����Ϊ����n��N*����$\sqrt{n}+\sqrt{n+2}��2\sqrt{n+1}$��֤�����£�
֤��һ��Ҫ֤��$\sqrt{n}+\sqrt{n+2}��2\sqrt{n+1}$
ֻ��֤��${��\sqrt{n}+\sqrt{n+2}��^2}��{��2\sqrt{n+1}��^2}$
��֤��$2n+2+2\sqrt{n}\sqrt{n+2}��4n+4$
Ҳ����֤��$\sqrt{n}\sqrt{n+2}��n+1$
ֻ��֤��n��n+2����n2+2n+1
��֤��0��1����Ȼ����
��$\sqrt{n}+\sqrt{n+2}��2\sqrt{n+1}$��
֤������$\sqrt{n+2}-\sqrt{n+1}$=$\frac{{��\sqrt{n+2}-\sqrt{n+1}����\sqrt{n+2}+\sqrt{n+1��}}}{{\sqrt{n+2}+\sqrt{n+1}}}$��
=$\frac{1}{{\sqrt{n+2}+\sqrt{n+1}}}$$\sqrt{n+1}-\sqrt{n}$��
=$\frac{{��\sqrt{n+1}-\sqrt{n}����\sqrt{n+1}+\sqrt{n}��}}{{\sqrt{n+1}+\sqrt{n}}}$��
=$\frac{1}{{\sqrt{n+1}+\sqrt{n}}}$��
��n��N*��$\sqrt{n+2}+\sqrt{n+1}��$$\sqrt{n+1}+\sqrt{n}��0$��
��$\frac{1}{{\sqrt{n+2}+\sqrt{n+1}}}��$$\frac{1}{{\sqrt{n+1}+\sqrt{n}}}$��
��$\sqrt{n+2}-\sqrt{n+1}��$$\sqrt{n+1}-\sqrt{n}$��
��$\sqrt{n}+\sqrt{n+2}��2\sqrt{n+1}$
���� ���⿼���˷��������ۺϷ����ؼ�����֤����ʽ�������е��⣮


 ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ���� | C�� | ���� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
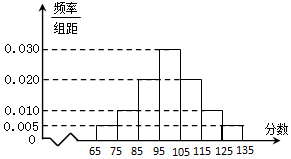 ijУ�߶��꼶��һ����ѧ����������ȡ�˲���ѧ������ѧ�ɼ����һ���������õ�����Ƶ�ʷֲ�ֱ��ͼ��
ijУ�߶��꼶��һ����ѧ����������ȡ�˲���ѧ������ѧ�ɼ����һ���������õ�����Ƶ�ʷֲ�ֱ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �� | C�� | �� | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m�Φ���m�Φ£�����Φ� | B�� | ��m�ͦ������ͦ£��� m�Φ� | ||
| C�� | ��m?����m�ͦ£��� ���ͦ� | D�� | ��m?�������ͦ£��� m�ͦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | c��b��a | B�� | c��a��b | C�� | a��b��c | D�� | a��c��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij�ֹ�˾���̻�һ��뾶Ϊ200�ף�Բ�Ľ�Ϊ$\frac{��}{4}$�����οյأ���ͼ������OPQ�������ε��ڽӾ���ABCDΪһˮ�أ�����ĵط��ֻ�������COP=��������ABCD�����ΪS����λ��ƽ���ף���
ij�ֹ�˾���̻�һ��뾶Ϊ200�ף�Բ�Ľ�Ϊ$\frac{��}{4}$�����οյأ���ͼ������OPQ�������ε��ڽӾ���ABCDΪһˮ�أ�����ĵط��ֻ�������COP=��������ABCD�����ΪS����λ��ƽ���ף����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a=b��c | B�� | b=c��a | C�� | a=c��b | D�� | a=b=c |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com