
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() 与
与![]() 的交点
的交点![]() 恰好是
恰好是![]() 中点,又
中点,又![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.

(![]() )求证:
)求证:![]() .
.
(![]() )求证:
)求证:![]() 平面
平面![]() .
.
(![]() )设平面
)设平面![]() 平面
平面![]() ,试问:直线
,试问:直线![]() 是否与直线
是否与直线![]() 平行,请说明理由.
平行,请说明理由.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】试题分析:(1)根据正三角形性质得![]() ,再根据线面垂直性质得
,再根据线面垂直性质得![]() ,由线面垂直判定定理得
,由线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() .(2)根据计算得
.(2)根据计算得![]() ,根据比例关系得
,根据比例关系得![]() ,再根据线面平行判定定理得结论,(3)先假设直线
,再根据线面平行判定定理得结论,(3)先假设直线![]() ,根据线面平行判定定理得
,根据线面平行判定定理得![]() 平面
平面![]() ,再根据线面平行性质定理得
,再根据线面平行性质定理得![]() ,与题意矛盾,否定假设.
,与题意矛盾,否定假设.
试题解析:(![]() )证明:∵
)证明:∵![]() 是正三角形,
是正三角形,![]() 是
是![]() 中点,
中点,
∴![]() ,即
,即![]() ,
,
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(![]() )在正三角形
)在正三角形![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() 为
为![]() 中点,
中点,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() .
.
在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(![]() )假设直线
)假设直线![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() ,
,
这与![]() 与
与![]() 不平行相矛盾,假设不成立.
不平行相矛盾,假设不成立.
∴直线![]() 与直线
与直线![]() 不平行.
不平行.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
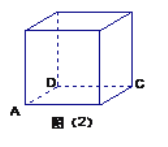
【题目】如图(1)是一正方体的表面展开图,MN和PB是两条面对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题。
(1)求证:MN∥平面PBD;
(2)求证:![]() 平面
平面![]() ;
;
(3)求PB和平面NMB所成的角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列{ ![]() }与{
}与{ ![]() },记A={
},记A={ ![]() |
| ![]() =
= ![]() ,
, ![]() },B={
},B={ ![]() |
| ![]() =
= ![]() ,
, ![]() },若同时满足条件:①{
},若同时满足条件:①{ ![]() },{
},{ ![]() }均单调递增;②
}均单调递增;② ![]() 且
且 ![]() ,则称{
,则称{ ![]() }与{
}与{ ![]() }是无穷互补数列.
}是无穷互补数列.
(1)若 ![]() =
= ![]() ,
, ![]() =
= ![]() ,判断{
,判断{ ![]() }与{
}与{ ![]() }是否为无穷互补数列,并说明理由;
}是否为无穷互补数列,并说明理由;
(2)若 ![]() =
= ![]() 且{
且{ ![]() }与{
}与{ ![]() }是无穷互补数列,求数列{
}是无穷互补数列,求数列{ ![]() }的前16项的和;
}的前16项的和;
(3)若{ ![]() }与{
}与{ ![]() }是无穷互补数列,{
}是无穷互补数列,{ ![]() }为等差数列且
}为等差数列且 ![]() =36,求{
=36,求{ ![]() }与{
}与{ ![]() }得通项公式.
}得通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】家用电器一件,现价2000元,实行分期付款,每期付款数相同,每期为一月,购买后一个月付款一次,共付12次,即购买后一年付清,如果按月利率8‰,每月复利一次计算,那么每期应付款多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
注:年份代码1﹣7分别对应年份2008﹣2014.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: ![]() =9.32,
=9.32, ![]() =40.17,
=40.17, ![]() =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
参考公式:  ,
,
回归方程 ![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于用斜二测画法画直观图的说法中,错误的是( )
A. 用斜二测画法画出的直观图是在平行投影下画出的空间图形
B. 几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同
C. 水平放置的矩形的直观图是平行四边形
D. 水平放置的圆的直观图是椭圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数是( )
①命题“x0∈R,x02+1>3x0”的否定是“x∈R,x2+1≤3x”;
②“函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
③x2+2x≥ax在x∈[1,2]上恒成立(x2+2x)min≥(ax)max在x∈[1,2]上恒成立;
④“平面向量 ![]() 与
与 ![]() 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“ ![]()
![]() <0”.
<0”.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点 P 与定点![]() 的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.
的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.
(1)求曲线 E 的方程;
(2)设 A 是曲线 E 上的一个点,直线 AF 交曲线 E 于另一点 B,以 AB 为边作一个平行四边形,顶点 A、B、C、D 都在轨迹 E 上,判断平行四边形 ABCD 能否为菱形,并说明理由;
(3)当平行四边形 ABCD 的面积取到最大值时,判断它的形状,并求出其最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com