
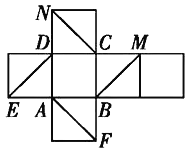
【题目】如图所示是一个正方体的平面展开图,在这个正方体中![]() 平面ADE;
平面ADE;![]() 平面ABF;
平面ABF;![]() 平面
平面![]() 平面AFN;
平面AFN;![]() 平面
平面![]() 平面NCF.以上四个命题中,真命题的序号是
平面NCF.以上四个命题中,真命题的序号是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
把正方体的平面展开图还原成正方体ABCA﹣EFMN,得出BM∥平面ADNE,判断①正确;由平面DCMN∥平面ABFE,得出CN∥平面ABFE,判断②正确;由BD∥FN,得出BD∥平面AFN,同理BM∥平面AFN,证明平面BDM∥平面AFN,判断③正确;由BD∥FN,BE∥CN,且BD∩BE=B,证明平面BDE∥平面NCF,判断④正确.
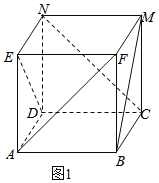
把正方体的平面展开图还原成正方体ABCA﹣EFMN,如图1所示;
对于①,平面BCMF∥平面ADNE,BM平面BCMF,
∴BM∥平面ADNE,①正确;
对于②,平面DCMN∥平面ABFE,CN平面DCMN,
∴CN∥平面ABFE,②正确;
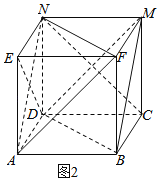
对于③,如图2所示,
BD∥FN,BD平面AFN,FN平面AFN,∴BD∥平面AFN;
同理BM∥平面AFN,且BD∩BM=B,
∴平面BDM∥平面AFN,③正确;
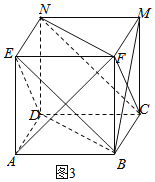
对于④,如图3所示,
BD∥FN,BE∥CN,BD∩BE=B,且BD、BE平面BDE,
∴平面BDE∥平面NCF,∴④正确.
综上,正确的命题序号是![]() .
.
故答案为:A.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的产品为优质品.现用A,B两种不同型号的节能灯做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示.
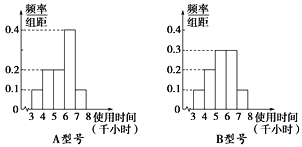
以上述试验结果中使用时间落入各组的频率作为相应的概率.
(1)现从大量的A,B两种型号节能灯中各随机抽取两件产品,求恰有两件是优质品的概率;
(2)已知A型节能灯的生产厂家对使用时间小于6千小时的节能灯实行“三包”.通过多年统计发现,A型节能灯每件产品的利润y(单位:元)与其使用时间t(单位:千小时)的关系如下表:
使用时间t(单位:千小时) | t<4 | 4≤t<6 | t≥6 |
每件产品的利润y(单位:元) | -10 | 10 | 20 |
若从大量的A型节能灯中随机抽取两件,其利润之和记为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆的极坐标方程为:ρ2-4![]() ρcos(θ-
ρcos(θ-![]() )+6=0.
)+6=0.
(1)将极坐标方程化为普通方程;
(2)若点P(x,y)在该圆上,求x+y的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2019年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图,给出下列4个结论
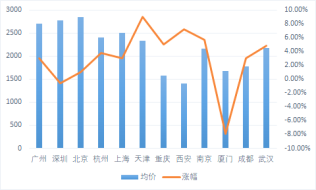
其中结论正确的是( )
A.深圳的变化幅度最小,北京的平均价格最高;
B.深圳和厦门往返机票的平均价格同去年相比有所下降;
C.平均价格从高到低位于前三位的城市为北京,深圳,广州;
D.平均价格的涨幅从高到低位于前三位的城市为天津,西安,上海.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax3-3ax,g(x)=bx2-ln x(a,b∈R),已知它们在x=1处的切线互相平行.
(1)求b的值;
(2)若函数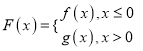 且方程F(x)=a2有且仅有四个解,求实数a的取值范围.
且方程F(x)=a2有且仅有四个解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市主办的科技知识竞赛的学生成绩中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组,第一组![]() ;第二组
;第二组![]() ;…;第六组
;…;第六组![]() ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.
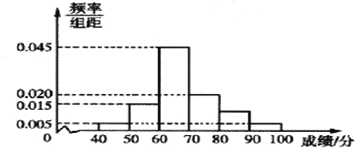
(1)求成绩在区间![]() 内的学生人数;
内的学生人数;
(2)从成绩大于等于80分的学生中随机选取2名,求至少有1名学生的成绩在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖促销活动,规定每位顾客从装有编号为0,1,2,3四个相同小球的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码之和等于6,则中一等奖,等于5中二等奖,等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com