
【题目】四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,PA=PD= ![]() ,E是BC中点,点Q在侧棱PC上.
,E是BC中点,点Q在侧棱PC上. 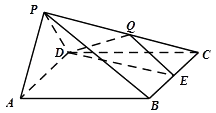
(1)求证:AD⊥PB;
(2)若Q是PC中点,求二面角E﹣DQ﹣C的余弦值;
(3)若 ![]() ,当PA∥平面DEQ时,求λ的值.
,当PA∥平面DEQ时,求λ的值.
【答案】
(1)证明:取AD中点O,连接OP,OB,BD.
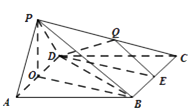
因为PA=PD,所以PO⊥AD.
因为菱形ABCD中,∠BCD=60°,所以AB=BD,所以BO⊥AD.
因为BO∩PO=O,所以AD⊥平面POB,所以AD⊥PB.
(2)解:由(1)知BO⊥AD,PO⊥AD.
因为侧面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,所以PO⊥底面ABCD.
以O为坐标原点,如图建立空间直角坐标系O﹣xyz.
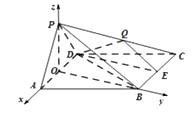
则D(﹣1,0,0), ![]() ,P(0,0,1),
,P(0,0,1), ![]() ,
,
因为Q为PC中点,所以 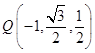 .
.
所以 ![]() ,
, 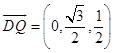 ,所以平面DEQ的法向量为
,所以平面DEQ的法向量为 ![]() .
.
因为 ![]() ,
, 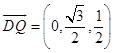 ,
,
设平面DQC的法向量为 ![]() ,则
,则  ,∴
,∴ 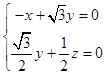
令 ![]() ,则y=1,
,则y=1, ![]() ,即
,即 ![]() .
. 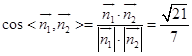 .
.
由图可知,二面角E﹣DQ﹣C为锐角,所以余弦值为 ![]() .
.
(3)解:因为 ![]() ,所以
,所以 ![]() ,
,
由(2)知 ![]() ,
, ![]() ,
,
若设Q(x,y,z),则 ![]() ,
,
由 ![]() ,得
,得 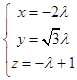 ,
,
在平面DEQ中, ![]() ,
, ![]() ,
,
所以平面DEQ法向量为 ![]() ,
,
又因为PA∥平面DEQ,所以 ![]() ,
,
即(1﹣λ)+(﹣1)(2λ﹣1)=0,得 ![]() .
.
所以,当 ![]() 时,PA∥平面DEQ.
时,PA∥平面DEQ.
【解析】(1)证明AD⊥平面POB,即可证明AD⊥PB;(2)证明PO⊥底面ABCD,建立空间直角坐标系,求出平面DEQ的法向量为 ![]() ,平面DQC的法向量
,平面DQC的法向量 ![]() ,利用向量的夹角公式,即可求得结论;(3)求出平面DEQ法向量为
,利用向量的夹角公式,即可求得结论;(3)求出平面DEQ法向量为 ![]() ,利用PA∥平面DEQ,即
,利用PA∥平面DEQ,即 ![]() ,从而可得结论.
,从而可得结论.
【考点精析】通过灵活运用直线与平面平行的判定和直线与平面垂直的性质,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;垂直于同一个平面的两条直线平行即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].将日均收看该类体育节目时间不低于40分钟的观众称为“体育迷”.则抽取的100名观众中“体育迷”有名. 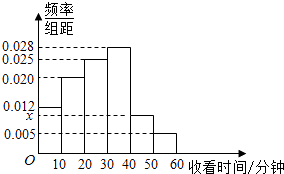
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)已知函数![]() ,
, ![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 是函数
是函数![]() 图象的切线,求
图象的切线,求![]() 的最小值;
的最小值;
(3)当![]() 时,若
时,若![]() 与
与![]() 的图象有两个交点
的图象有两个交点![]() ,求证:
,求证: ![]()
![]() .(取
.(取![]() 为
为![]() ,取
,取![]() 为
为![]() ,取
,取![]() 为
为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx+c在点x=2处取得极值c﹣16. (Ⅰ)求a,b的值;
(Ⅱ)若f(x)有极大值28,求f(x)在[﹣3,3]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设对于任意实数x,不等式|x+7|+|x﹣1|≥m恒成立.
(1)求m的取值范围;
(2)当m取最大值时,解关于x的不等式:|x﹣3|﹣2x≤2m﹣12.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了实施政府绩效管理、创新政府公共服务模式、提高公共服务效率.实施了“政府承诺,等你打分”民意调查活动,通过问卷调查了学生、在职人员、退休人员共250人,统计结果表不幸被污损,如表:
学生 | 在职人员 | 退休人员 | |
满意 |
|
| 78 |
不满意 | 5 |
| 12 |
若在所调查人员中随机抽取1人,恰好抽到学生的概率为0.32.
(1)求满意学生的人数;
(2)现用分层抽样的方法在所调查的人员中抽取25人,则在职人员应抽取多少人?
(3)若满意的在职人员为77,则从问卷调查中填写不满意的“学生和在职人员”中选出2人进行访谈,求这2人中包含了两类人员的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 。
。
(1)若f(x)的图象与g(x)的图象所在两条曲线的一个公共点在y轴上,且在该点处两条曲线的切线互相垂直,求b和c的值。
(2)若a=c=1,b=0,试比较f(x)与g(x)的大小,并说明理由;
(3)若b=c=0,证明:对任意给定的正数a,总存在正数m,使得当x![]() 时,
时,
恒有f(x)>g(x)成立。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 点(n, ![]() )在直线y=
)在直线y= ![]() x+
x+ ![]() 上. (Ⅰ)求数列{an}的通项公式;
上. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和为Tn , 并求使不等式Tn>
,求数列{bn}的前n项和为Tn , 并求使不等式Tn> ![]() 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com