
【题目】已知函数![]() ,
, 若关于
若关于![]() 的方程
的方程![]() 有两个不等实数根
有两个不等实数根![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:由题意首先确定函数f(x)的性质,然后结合函数的性质将二元问题转化为一元问题,最后利用导函数构造函数确定最值即可.
详解:因为f(x)=x3+sinx是奇函数且f′(x)=3x2+cosx≥0,所以f(x)=x3+sinx单调递增,
若关于x的方程f(g(x))+m=0恰有两个不等实根![]() ,
,
等价于f(t)+m=0有且只有一个根,t=g(x)有且只有两个根![]() ,
,
且![]() ,
,
所以![]() ,
,
设函数t(x)=x-2ln(x+l)+2,则![]() ,
,
所以当0<x<1时,t′(x)<0,t(x)单调递减,
当x>1时,t′(x)>0,t(x)单调递增,
所以,f(x)的极小值即最小值是t(1)=3-21n2,即![]() 的最小值为3-2ln2.
的最小值为3-2ln2.
本题选择D选项.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】现有一块大型的广告宣传版面,其形状是右图所示的直角梯形![]() .某厂家因产品宣传的需要,拟投资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形
.某厂家因产品宣传的需要,拟投资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形![]() (点
(点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() 在线段
在线段![]() 上).已知
上).已知![]() ,
, ![]() ,其中曲线段
,其中曲线段![]() 是以
是以![]() 为顶点,
为顶点, ![]() 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.

(1)建立适当的平面直角坐标系,分别求出曲线段![]() 与线段
与线段![]() 的方程;
的方程;
(2)求该厂家广告区域![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
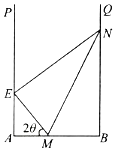
【题目】某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分隔线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分隔线总长度为l.
(1)设∠AME=2θ,求用θ表示的l函数表达式,并写出定义域;
(2)求l的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
A.f(x)= ![]()
B.f(x)=x3
C.f(x)=( ![]() )x
)x
D.f(x)=3x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( ) 
A.y= ![]() ﹣
﹣ ![]() x
x
B.y= ![]() x3﹣
x3﹣ ![]() x
x
C.y= ![]() x3﹣x
x3﹣x
D.y=﹣ ![]() x3+
x3+ ![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四面体ABCD及其三视图(如图2所示),过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H. 
(1)证明:四边形EFGH是矩形;
(2)求直线AB与平面EFGH夹角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球台面被网分成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D,某次测试要求队员接到落点在甲上的来球后向乙回球,规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,小明回球的落点在C上的概率为 ![]() ,在D上的概率为
,在D上的概率为 ![]() ;对落点在B上的来球,小明回球的落点在C上的概率为
;对落点在B上的来球,小明回球的落点在C上的概率为 ![]() ,在D上的概率为
,在D上的概率为 ![]() .假设共有两次来球且落在A,B上各一次,小明的两次回球互不影响,求:
.假设共有两次来球且落在A,B上各一次,小明的两次回球互不影响,求: 
(1)小明两次回球的落点中恰有一次的落点在乙上的概率;
(2)两次回球结束后,小明得分之和ξ的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 、
、![]() 、
、![]() 是同一平面上不共线的四点,若存在一组正实数
是同一平面上不共线的四点,若存在一组正实数![]() 、
、![]() 、
、![]() ,使得
,使得![]() ,则三个角
,则三个角![]() 、
、![]() 、
、![]() ( )
( )
A. 都是钝角B. 至少有两个钝角
C. 恰有两个钝角D. 至多有两个钝角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com