
【题目】如图,一块弓形余布料EMF,点M为弧![]() 的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=
的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=![]() .将弓形余布料裁剪成尽可能大的矩形ABCD(不计损耗), AD∥EF,且点A、D在弧
.将弓形余布料裁剪成尽可能大的矩形ABCD(不计损耗), AD∥EF,且点A、D在弧![]() 上,设∠AOD=
上,设∠AOD=![]() .
.
(1)求矩形ABCD的面积S关于![]() 的函数关系式;
的函数关系式;
(2)当矩形ABCD的面积最大时,求cos![]() 的值.
的值.
【答案】(1) 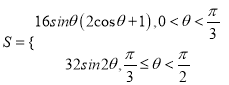 (2) cosθ=
(2) cosθ=![]()
【解析】试题分析: ![]() 分类讨论,求出
分类讨论,求出![]() ,可得矩形
,可得矩形![]() 的面积与关于
的面积与关于![]() 的函数解析式。
的函数解析式。
![]() 求导确定函数的单调性,即可求
求导确定函数的单调性,即可求![]() 的值。
的值。
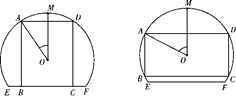
解析:(1) 设矩形铁片的面积为S,∠AOM=θ.
当0<θ<![]() 时(如图1),AB=4cosθ+2,AD=2×4sinθ,
时(如图1),AB=4cosθ+2,AD=2×4sinθ,
S=AB×AD= (4cosθ+2)(2×4sinθ)=16sinθ(2cosθ+1).
当![]() ≤θ<
≤θ<![]() 时(如图2),AB=2×4cos θ,AD=2×4sin θ,
时(如图2),AB=2×4cos θ,AD=2×4sin θ,
故S=AB×AD=64sinθcosθ=32sin 2θ.
综上得,矩形铁片的面积S关于θ的函数关系式为
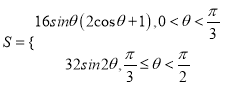
(2) 当0<θ<![]() 时,求导,得S′=16[cosθ(2cosθ+1)+sinθ(-2sinθ)]
时,求导,得S′=16[cosθ(2cosθ+1)+sinθ(-2sinθ)]
=16(4cos2 θ+cos θ-2).
令S′=0,得cosθ=![]() . 记区间
. 记区间![]() 内余弦值等于
内余弦值等于![]() 的角为θ0(唯一存在),
的角为θ0(唯一存在),
列表:
θ | (0,θ0) | θ0 |
|
S′ | + | 0 | - |
S | 极大值 |
又当![]() ≤θ<
≤θ<![]() 时,S=32sin2θ是单调减函数,所以当θ=θ0,即cosθ=
时,S=32sin2θ是单调减函数,所以当θ=θ0,即cosθ=![]() 时,矩形铁片的面积最大.
时,矩形铁片的面积最大.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边长分别是a,b,c.满足2acosC+ccosA=b.
(Ⅰ)求角C的大小;
(Ⅱ)求sinAcosB+sinB的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是各项都为正数的等比数列,{bn}是等差数列,且a1=b1=1,a3+b5=13,a5+b3=21.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn , 求数列{Snbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租地建仓库,每月土地占用费y1与车库到车站的距离x成反比,而每月的库存货物的运费y2与车库到车站的距离x成正比.如果在距离车站10公里处建立仓库,这两项费用y1和y2分别为2万元和8万元.求若要使得这两项费用之和最小时,仓库应建在距离车站多远处?此时最少费用为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
(Ⅰ)证明:A1C1=AB1;
(Ⅱ)若AC⊥AB1 , ∠BCC1=120°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值.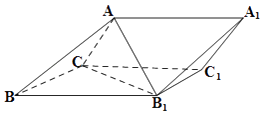
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为 . 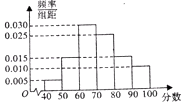
查看答案和解析>>
科目:高中数学 来源: 题型:
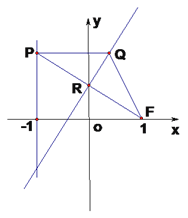
【题目】在平面直角坐标系![]() 中,设点
中,设点![]() (1,0),直线
(1,0),直线![]() :
: ![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动, ![]() 是线段
是线段![]() 与
与![]() 轴的交点, 异于点R的点Q满足:
轴的交点, 异于点R的点Q满足: ![]() ,
, ![]() .
.
(1)求动点![]() 的轨迹的方程;
的轨迹的方程;
(2) 记![]() 的轨迹的方程为
的轨迹的方程为![]() ,过点
,过点![]() 作两条互相垂直的曲线
作两条互相垂直的曲线![]()
的弦![]() .
. ![]() ,设
,设![]() .
. ![]() 的中点分别为
的中点分别为![]() .
.
问直线![]() 是否经过某个定点?如果是,求出该定点,
是否经过某个定点?如果是,求出该定点,
如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系中, ![]() 为极点,半径为2的圆
为极点,半径为2的圆![]() 的圆心坐标为
的圆心坐标为![]() .
.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设直角坐标系的原点与极点![]() 重合,
重合, ![]() 轴非负关轴与极轴重合,直线
轴非负关轴与极轴重合,直线![]() 的参数方程为
的参数方程为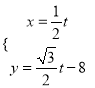 (
(![]() 为参数),由直线
为参数),由直线![]() 上的点向圆
上的点向圆![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com