
【题目】四棱锥S-ABCD中,底面ABCD是边长为2的菱形,![]() ,
,![]() ,二面角S-BD-C的余弦值为
,二面角S-BD-C的余弦值为![]() .
.
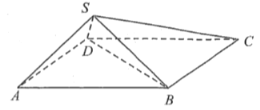
(I)证明:平面![]() 平面SBD;
平面SBD;
(Ⅱ)求二面角A-SD-C的余弦值.
【答案】(I)见解析(Ⅱ)![]()
【解析】
(I) 连接AC,交BD于点O.连接SO易证得![]() ,
,![]() 即
即![]() 平面SAO,得到
平面SAO,得到![]() ,利用余弦定理解得
,利用余弦定理解得![]() ,由
,由![]() 可证得
可证得![]() ,即可得到
,即可得到![]() 平面SBD,即可证得结论;
平面SBD,即可证得结论;
(Ⅱ)建系,设![]() 和
和![]() 分别为平面SAD、平面SCD的法向量,求出法向量,利用公式计算即可得出结果.
分别为平面SAD、平面SCD的法向量,求出法向量,利用公式计算即可得出结果.
(Ⅰ)连接AC,交BD于点O.连接SO菱形ABCD中,![]() ,且O是AC和BD的中点.
,且O是AC和BD的中点.
因为![]() ,所以
,所以![]() ,
,
![]() 是二面角S-BD-C的平面角,
是二面角S-BD-C的平面角,
即![]() ,
,![]() .
.
又![]() ,所以
,所以![]() 平面SAC,
平面SAC,![]() .
.
![]() 中,由余弦定理知:
中,由余弦定理知:
![]() .
.
所以![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面SBD,
平面SBD,
又![]() 平面SAB,所以平面SAB⊥平面SBD.
平面SAB,所以平面SAB⊥平面SBD.
(Ⅱ)如图,分别以![]() ,
,![]() 为x,y轴的正方向,建立空间直角坐标系
为x,y轴的正方向,建立空间直角坐标系![]() .
.
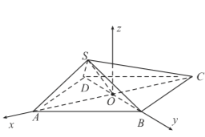
则点![]() ,
,![]()
![]()
![]()
 ,
,
![]() ,
,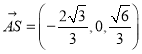 ,
,
![]() ,
, .
.
设![]() 和
和![]() 分别为平面SAD、平面SCD的法向量,
分别为平面SAD、平面SCD的法向量,
则由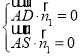 ,得
,得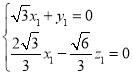 ,
,
取![]() ,
,
由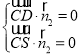 ,得
,得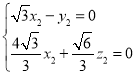 .
.
取![]() .
.
 .
.
故二面角A-SD-C的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,如图,
,如图,![]() 分别交
分别交![]() 轴正半轴于点
轴正半轴于点![]() .射线
.射线![]() 分别交
分别交![]() 于点
于点![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 轴垂直,直线
轴垂直,直线![]() 与
与![]() 轴垂直.
轴垂直.

(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交曲线
交曲线![]() 与点
与点![]() ,射线
,射线![]() 与点
与点![]() ,且交曲线
,且交曲线![]() 于点
于点![]() .问:
.问:![]() 的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,过曲线![]() 外的一点
外的一点![]() (其中
(其中![]() ,
,![]() 为锐角)作平行于
为锐角)作平行于![]() 的直线
的直线![]() 与曲线分别交于
与曲线分别交于![]() .
.
(Ⅰ) 写出曲线![]() 和直线
和直线![]() 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为![]() 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别在线段
分别在线段![]() 和
和![]() 上,且
上,且![]() ,
,![]() 为
为![]() 中点,以
中点,以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且平面
的位置,且平面![]() 平面
平面![]() .
.
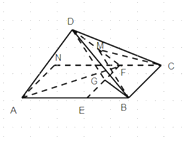
(1)求证:平面![]() 平面
平面![]() ;
;
(2)点![]() 为线段
为线段![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c为正数,f(x)=|x+a|+|x+b|+|x﹣c|.
(1)若a=b=c=1,求函数f(x)的最小值;
(2)若f(0)=1且a,b,c不全相等,求证:b3c+c3a+a3b>abc.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() ,
,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,是否存在整数
轴,是否存在整数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出
时恒成立?若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甘肃省是土地荒漠化较为严重的省份,一代代治沙人为了固沙、治沙,改善生态环境,不断地进行研究与实践,实现了沙退人进.![]() 年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了
年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了![]() 个风蚀插钎,以测量风蚀值.(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为
个风蚀插钎,以测量风蚀值.(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为![]() 表示该插钎处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.
表示该插钎处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.
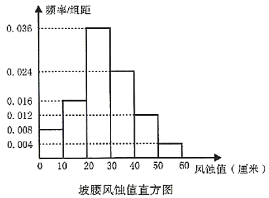
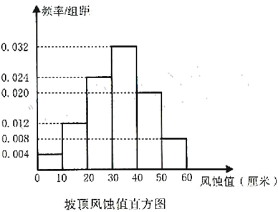
(Ⅰ)根据直方图估计“坡腰处一个插钎风蚀值小于![]() ”的概率;
”的概率;
(Ⅱ)若一个插钎的风蚀值小于![]() ,则该数据要标记“
,则该数据要标记“![]() ”,否则不标记根据以上直方图,完成列联表:
”,否则不标记根据以上直方图,完成列联表:
标记 | 不标记 | 合计 | |
坡腰 | |||
坡顶 | |||
合计 |
并判断是否有![]() 的把握认为数据标记“
的把握认为数据标记“![]() ”与沙丘上插钎所布设的位置有关?
”与沙丘上插钎所布设的位置有关?
附: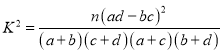 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂根据市场需求开发三角花篮支架(如图),上面为花篮,支架由三根细钢管组成,考虑到钢管的受力和花篮质量等因素,设计支架应满足:①三根细钢管长均为1米(粗细忽略不计),且与地面所成的角均为![]() ;②架面与架底平行,且架面三角形
;②架面与架底平行,且架面三角形![]() 与架底三角形
与架底三角形![]() 均为等边三角形;③三根细钢管相交处的节点
均为等边三角形;③三根细钢管相交处的节点![]() 分三根细钢管上、下两段之比均为
分三根细钢管上、下两段之比均为![]() .定义:架面与架底的距离为“支架高度”,架底三角形
.定义:架面与架底的距离为“支架高度”,架底三角形![]() 的面积与“支架高度”的乘积为“支架需要空间”.
的面积与“支架高度”的乘积为“支架需要空间”.
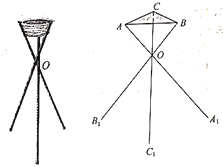
(1)当![]() 时,求“支架高度”;
时,求“支架高度”;
(2)求“支架需要空间”的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com