
 如图在四棱台ABCD-A1B1C1D1中,AA1⊥平面ABCD,两底面均为正方形,AB=AA1=2A1B1.
如图在四棱台ABCD-A1B1C1D1中,AA1⊥平面ABCD,两底面均为正方形,AB=AA1=2A1B1.分析 (1)连结AC,交BD于O,连结A1O,连结A1C1,由已知得OCC1A1是平行四边形,从而A1C∥C1C,由此能证明CC1∥平面A1BD.
(2)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出在线段CC1上存在一点P,使得AP⊥平面A1BD,且$\frac{CP}{P{C}_{1}}$=2.
解答 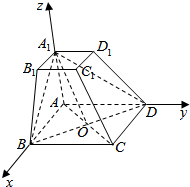 证明:(1)连结AC,交BD于O,连结A1O,连结A1C1,
证明:(1)连结AC,交BD于O,连结A1O,连结A1C1,
∵在四棱台ABCD-A1B1C1D1中,AA1⊥平面ABCD,两底面均为正方形,AB=AA1=2A1B1,
∴A1C1∥OC,且A1C1OC,
∴OCC1A1是平行四边形,∴A1C∥C1C,
∵CC1?平面A1BD,OA1?平面A1BD,
∴CC1∥平面A1BD.
解:(2)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
假设线段CC1上是否存在一点P(a,b,c),使得AP⊥平面A1BD,且$\frac{CP}{P{C}_{1}}$=λ,
设AB=AA1=2A1B1=2,
则A(0,0,0),C(2,2,0),C1(1,1,2),
$\overrightarrow{CP}$=(a-2,b-2,c),$\overrightarrow{P{C}_{1}}$=(1-a,1-b,2-c),
∴$\left\{\begin{array}{l}{a-2=λ(1-a)}\\{b-2=λ(1-b)}\\{c=λ(2-c)}\end{array}\right.$,∴P($\frac{λ+2}{λ+1}$,$\frac{λ+2}{λ+1}$,$\frac{2λ}{λ+1}$),
A1(0,0,2),B(2,0,0),D(0,2,0),
$\overrightarrow{{A}_{1}B}$=(2,0,-2),$\overrightarrow{{A}_{1}D}$=(0,2,-2),$\overrightarrow{AP}$=($\frac{λ+2}{λ+1}$,$\frac{λ+2}{λ+1}$,$\frac{2λ}{λ+1}$),
∵AP⊥平面A1BD,
∴2×$\frac{λ+2}{λ+1}$-2×$\frac{2λ}{λ+1}$=0,解得λ=2,
∴在线段CC1上存在一点P,使得AP⊥平面A1BD,且$\frac{CP}{P{C}_{1}}$=2.
点评 本题考查线面平行的证明,考查在直线上是否存在使得线面垂直的点的判断与求法,是中档题,解题时要认真审题,注意空间思维能力的培养和向量法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{61}$ | B. | $\sqrt{41}$ | C. | 2$\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-2 | D. | -2-$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北冀州市高二文上月考三数学试卷(解析版) 题型:解答题
如图,已知定圆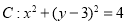 ,定直线
,定直线 ,过
,过 的一条动直线
的一条动直线 与直线相交于
与直线相交于 ,与圆
,与圆 相交于
相交于 ,
, 两点,
两点, 是
是 中点.
中点.
(Ⅰ)当 与
与 垂直时,求证:
垂直时,求证: 过圆心
过圆心 ;
;
(Ⅱ)当 时,求直线
时,求直线 的方程;
的方程;
(Ⅲ)设 ,试问
,试问 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com