
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.分析 (1)解法一:以D为坐标原点,分别以$\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{DP}$所在的方向为x轴,y轴,z轴的正方向,建立空间直角坐标系D-xyz.求出相关点的坐标.
法一,推出$\overrightarrow{PA}=\overrightarrow{DB}-2\overrightarrow{DE}$.然后证明PA∥平面EDB.
法二:取BD的中点G,则G(1,1,0),利用$\overrightarrow{PA}=2$$\overrightarrow{EG}$,说明PA∥EG.证明PA∥平面EDB.
法三:求出平面EDB的一个法向量$\overrightarrow{n}$,证明$\overrightarrow{PA}⊥\overrightarrow{n}$,推出PA∥平面EDB.
解法二:连接AC,设AC∩BD=G.证明PA∥EG.然后证明PA∥平面EDB.
(2)解法一:由(1)中的解法一,求出平面CPB的一个法向量$\overrightarrow{m}$,证明AC⊥BD.PD⊥AC.推出AC⊥平面PDB.
求出平面PDB的一个法向量,利用空间向量的数量积求解锐二面角C-PB-D的大小.
解法二:过G作GF⊥PB于F,连接FC.说明∠GFC就是二面角C-PB-D的一个平面角通过求解三角形即可.
解答 (1)解法一:如图,以D为坐标原点,分别以$\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{DP}$所在的方向为x轴,y轴,z轴的正方向,建立空间直角坐标系D-xyz.
则A(2,0,0),P(0,0,2),D(0,0,0),B(2,2,0),C(0,2,0),E(0,1,1).…(2分)
法一:$\overrightarrow{PA}=(2,0,-2),\overrightarrow{DB}=(2,2,0),\overrightarrow{DE}=(0,1,1)$.
设$\overrightarrow{PA}=λ\overrightarrow{DB}+μ\overrightarrow{DE}$,即(2,0,-2)=λ(2,2,0)+μ(0,1,1).
解得λ=1,μ=-2.
所以$\overrightarrow{PA}=\overrightarrow{DB}-2\overrightarrow{DE}$.
又PA?平面EDB,所以PA∥平面EDB.…(4分)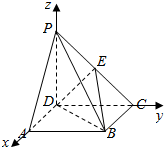
法二:取BD的中点G,则G(1,1,0).$\overrightarrow{PA}=(2,0,-2)$,$\overrightarrow{EG}=(1,0,-1)$.
所以$\overrightarrow{PA}=2$$\overrightarrow{EG}$,所以PA∥EG.
又PA?平面EDB,EG?平面EDB,
所以PA∥平面EDB.…(4分)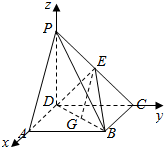
法三:$\overrightarrow{DB}=(2,2,0),\overrightarrow{DE}=(0,1,1)$.
设$\overrightarrow{n}$=(x,y,z)为平面EDB的一个法向量,
则$\overrightarrow{n}•\overrightarrow{DB}=0,\overrightarrow{n}•\overrightarrow{DE}=0$,即2x+2y=0,y+z=0.
取y=-1,则x=z=1.于是$\overrightarrow{n}$=(1,-1,1).
又$\overrightarrow{PA}=(2,0,-2)$,所以$\overrightarrow{n}•\overrightarrow{PA}=1×2+(-1)×0+1×(-2)=0$.所以$\overrightarrow{PA}⊥\overrightarrow{n}$.
又PA?平面EDB,所以PA∥平面EDB.…(4分)
解法二:连接AC,设AC∩BD=G.
因为ABCD是正方形,所以G是线段AC的中点.
又E是线段PC的中点,所以,EG是△PAC的中位线.
所以PA∥EG.…(2分)
又PA?平面EDB,EG?平面EDB,
所以PA∥平面EDB.…(4分)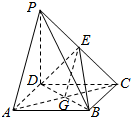
(2)解法一:由(1)中的解法一,$\overrightarrow{PB}=(2,2,-2)$,$\overrightarrow{CB}=(2,0,0)$.
设$\overrightarrow{m}$=(x1,y1,z1)为平面CPB的一个法向量,
则$\overrightarrow{m}•\overrightarrow{PB}=2{x}_{1}+2{y}_{1}-2{z}_{1}=0$,$\overrightarrow{m}•\overrightarrow{CB}=2{x}_{1}=0$.
取y1=1,则z1=1.于是$\overrightarrow{m}$=(0,1,1).…(7分)
因为ABCD是正方形,所以AC⊥BD.
因为PD⊥底面ABCD,所以PD⊥AC.
又PD∩BD=D,所以AC⊥平面PDB.
所以$\overrightarrow{AC}=(-2,2,0)$是平面PDB的一个法向量.…(10分)
所以$cos<\overrightarrow{m},\overrightarrow{AC}>=\frac{2}{\sqrt{2}×2\sqrt{2}}=\frac{1}{2}$.…(11分)
所以,锐二面角C-PB-D的大小为60°.…(12分)
解法二:如图,设AC∩BD=G.
在Rt△PDB中,过G作GF⊥PB于F,连接FC.…(5分)
因为四边形ABCD是正方形,
所以CA⊥BD,即CG⊥BD.…(6分)
因为侧棱PD⊥底面ABCD,CG?平面ABCD,
所以CG⊥PD.…(7分)
又CG⊥BD,PD∩BD=D,所以CG⊥平面PDB.
所以CG⊥PB.…(8分)
又PB⊥GF,CG∩GF=G,所以PB⊥平面CGF.
所以PB⊥FC.从而∠GFC就是二面角C-PB-D的一个平面角…(9分)
在Rt△PDB中,$FG=BG•sin∠GBF=BG•\frac{PD}{PB}=\sqrt{2}×\frac{2}{{\sqrt{{2^2}+{{(2\sqrt{2})}^2}}}}=\frac{{\sqrt{2}}}{{\sqrt{3}}}$.…(11分)
在Rt△FGC中,$tan∠GFC=\frac{GC}{FG}=\frac{{\sqrt{2}}}{{\frac{{\sqrt{2}}}{{\sqrt{3}}}}}=\sqrt{3}$.所以∠GFC=60°.
所以二面角C-PB-D的大小为60°.…(12分)
点评 本题考查二面角的平面角的求法,直线与平面平行的判定定理的应用,考查逻辑推理能力以及计算能力.


科目:高中数学 来源: 题型:选择题
 如图,PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上的一点,AE⊥PB于点E,AF⊥PC于点F,对于下列说法,正确的个数是( )
如图,PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上的一点,AE⊥PB于点E,AF⊥PC于点F,对于下列说法,正确的个数是( )| A. | 4 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
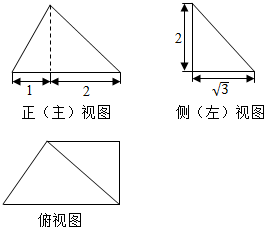
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{5\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{7\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com