
(1)����f(x)�ĵ����������Сֵ;
(2)��b��0ʱ����֤:bb��![]() (����e=2.718 28������Ȼ�����ĵ���);
(����e=2.718 28������Ȼ�����ĵ���);
(3)��a��0,b��0��֤��f(a)+(a+b)ln2��f(a+b)-f(b).
(��)��֪����m=(x2,y-cx),n=(1,x+b)(x,y,b,c��R)��m��n,������x,y������Ĺ�ϵʽ��Ϊy=f(x).��f��(x)Ϊf(x)�ĵ�����,F(x)=f(x)+af��(x)(a��0),��F(x)��R�ϵ��溯��.
(1)��![]() ��c��ֵ.
��c��ֵ.
(2)����f(x)�ĵ����ݼ�����(����ĸa��ʾ).
(3)��a=2ʱ,��0��t��4��t��2,����y=f(x)�ڵ�A(t,f(t))��������������y=f(x)�ཻ�ڵ�B(m,f(m))(A��B���غ�),ֱ��x=t��y=f(m)�ཻ�ڵ�C,��ABC�����ΪS,����t��ʾ��ABC�����S(t),����S(t)�����ֵ.
�𰸣�(��)��:(1)��f��(x)=lnx+1(x��0),
��f��(x)��0,��lnx��-1=lne-1.��e=2.718 28����1,��y=lnx��(0,+��)���ǵ�����������.
��x��e-1=![]() .��x�ʣ�
.��x�ʣ�![]() ,+��).ͬ��,��f��(x)��0�ɵ�x��(0,
,+��).ͬ��,��f��(x)��0�ɵ�x��(0,![]() ��.��f(x)�ĵ�����������Ϊ��
��.��f(x)�ĵ�����������Ϊ��![]() ,+��),�����ݼ�����Ϊ(0,
,+��),�����ݼ�����Ϊ(0,![]() ��.
��.
�ɴ˿�֪y=f(x)min=f(![]() )=
)=![]() .
.
(2)֤��:��(1)��֪��b��0ʱ,��f(b)��f(x)min=![]() ,��blnb��
,��blnb��![]() ,
,
��ln(bb)��![]() =ln(
=ln(![]() )
)![]() .��bb��(
.��bb��(![]() )
)![]() .
.
(3)֤��:��f(a)+(a+b)ln2��f(a+b)-f(b)����,��f(a)+f(b)��f(a+b)-(a+b)ln2,
��֤f(a)+f(a+b-a)��f(a+b)-(a+b)ln2.�躯��g(x)=f(x)+f(k-x)(k��0).
��f(x)=xlnx,��g(x)=xlnx+(k-x)ln(k-x).��0��x��k.��g��(x)=lnx+1-ln(k-x)-1=ln![]() ,
,
��g��(x)��0,����![]() ��1
��1![]()
![]() ��0
��0![]()
![]() ��x��k.
��x��k.
�ຯ��g(x)�ڣ�![]() ,k)�ϵ�������,��(0,
,k)�ϵ�������,��(0,![]() ���ϵ����ݼ�.��g(x)����СֵΪg(
���ϵ����ݼ�.��g(x)����СֵΪg(![]() ),������g(x)��g(
),������g(x)��g(![]() ).��g(
).��g(![]() )=f(
)=f(![]() )+f(k-
)+f(k-![]() )=kln
)=kln![]() =k(lnk-ln2)=f(k)-kln2,��g(x)��f(k)-kln2,
=k(lnk-ln2)=f(k)-kln2,��g(x)��f(k)-kln2,
��f(x)+f(k-x)��f(k)-kln2.��x=a,k-x=b,��k=a+b.��f(a)+f(b)��f(a+b)-(a+b)ln2.
��f(a)+(a+b)ln2��f(a+b)-f(b).
(��)�⣺(1)��f(x)=x3+bx2+cxz��f��(x)=3x2+2bx+c.
��F(x)=f(x)+af��(x)=x3+(b+3a)x2+(c+2ab)x+acΪ�溯��,��F(-x)=-F(x),�ɵ�b+3a=0,ac=0.
��a��0,��b=-3a,c=0.��![]() =-3,c=0.
=-3,c=0.
(2)��(1)�ɵ�f(x)=x3-3ax2,��f��(x)=3x(x-2a).��3x(x-2a)��0,���0��x��2a.�ຯ��f(x)�ĵ����ݼ�����Ϊ��0,2a��.
(3)��a=2ʱ,����y=f(x)�ڵ�A(t,f(t))�������߷���Ϊy-f(t)=f��(t)(x-t),kAB=f��(t)=3t(t-4).
����������![]() ����,��f(x)-f(t)=f��(t)(x-t),
����,��f(x)-f(t)=f��(t)(x-t),
��x3-6x2-t3+6t2=(3t2-12t)(x-t),(x-t)(x2+xt+t2-6x-6t)=(x-t)(3t2-12t).
��A��B���غ�,��x��t.��x2+xt+t2-6x-6t=3t2-12t.��x2+(t-6)x-2t2+6t=0,
��(x-t)(x+2t-6)=0.��x��t,��x=-2t+6.����һ����ΪB(m,f(m)),��m=-2t+6.
S(t)=![]() |m-t|��|f(m)-f(t)|=
|m-t|��|f(m)-f(t)|=![]() (m-t)2��|kAB|=
(m-t)2��|kAB|=![]() (t-2)2��3t(4-t)=
(t-2)2��3t(4-t)=![]() (t-2)2(4-t)t,����t��(0,2)��(2,4).
(t-2)2(4-t)t,����t��(0,2)��(2,4).
��h(t)=(t-2)2(4-t)t,����t��(0,2)��(2,4).��h(t)=-(t4-8t3+20t2-16t),
��h��(t)=-4(t3-6t2+10t-4)=-4(t-2)(t-2+![]() )(t-2-
)(t-2-![]() ).
).
��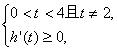 ���0��t��2-
���0��t��2-![]() ,��2��t��2+
,��2��t��2+![]() .
.
���Ǻ���h(t)������(0,2-![]() �ݡ�(2,2+
�ݡ�(2,2+![]() �����ǵ���������;�������2-
�����ǵ���������;�������2-![]() ,2)����2+
,2)����2+![]() ,4)���ǵ���������.��t=2-
,4)���ǵ���������.��t=2-![]() ��t=2+
��t=2+![]() ʱ,����y=h(t)�м���ֵ.
ʱ,����y=h(t)�м���ֵ.
��h(t)max=h(2-![]() )=h(2+
)=h(2+![]() )=4.��S(t)max=54.
)=4.��S(t)max=54.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�

 ��������֪����f(x)=
��������֪����f(x)=| ln(2-x2) |
| |x+2|-2 |
| AB |
| AD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| sin2x-(a-4)(sinx-cosx)+a |
| �� |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2011•��������ģ����������֪����f(x)=
��2011•��������ģ����������֪����f(x)=| ln(2-x2) | |x+2|-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ||
| 1-x |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| sin�� | ||
|
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com