
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为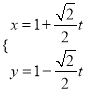 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 点的直角坐标为
点的直角坐标为![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求![]() 的值.
的值.
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
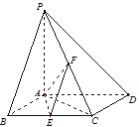
【题目】如图,已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() 的中点.
的中点.
(Ⅰ)证明: ![]() ;
;
(Ⅱ)若![]() 为
为![]() 上的动点,
上的动点, ![]() 与平面
与平面![]() 所成最大角的正切值为
所成最大角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣a)(x﹣b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=ax+b的图象大致为( ) 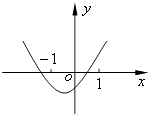
A.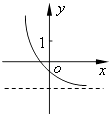
B.
C.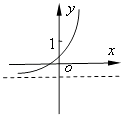
D.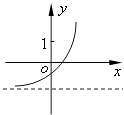
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),当x>0时,f(x)=﹣x2+2x
(1)求函数f(x)在R上的解析式;
(2)若函数f(x)在区间[﹣1,a﹣2]上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大理石工厂初期花费98万元购买磨大理石刀具,第一年需要各种费用12万元,从第二年起,每年所需费用比上一年增加4万元,该大理石加工厂每年总收入50万元.
(1)到第几年末总利润最大,最大值是多少?
(2)到第几年末年平均利润最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c(a≠0)的图象过点(0,1)且与x轴有唯一的交点(﹣1,0).
(1)求f(x)的表达式;
(2)在(1)的条件下,设函数F(x)=f(x)﹣mx,若F(x)在区间[﹣2,2]上是单调函数,求实数m的取值范围;
(3)设函数g(x)=f(x)﹣kx,x∈[﹣2,2],记此函数的最小值为h(k),求h(k)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本为0.5万元,但每生产1百台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为5百台,销售的收入(单位:万元)函数为:R(x)=5x﹣ ![]() x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
(1)将利润表示为产量的函数;
(2)年产量是多少时,企业所得利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com