
(1)求证:PA·PB=PO·PE;
(2)若DE⊥CF,∠P=15°,⊙O的半径为2,求CF的长.
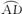
图2-6
思路分析:由PA·PB立刻想起割线定理.只需证PC·PD=PO·PE.
(1)证明:连结OD.
∵DF⊥AB,∴![]() =
=![]() .
.
又∠AOD度数等于![]() 度数的一半,∠DCF度数等于
度数的一半,∠DCF度数等于![]() 度数的一半,
度数的一半,
∴∠AOD=∠DCF.
∴180°-∠AOD=180°-∠DCF.
∴∠POD=∠PCE,∠P为公共角.
∴△PCE∽△POD.∴![]() .
.
∴PC·PD=PO·PE.
由割线定理PC·PD=PA·PB,
∴PA·PB=PO·PE.
(2)解析:∵AB⊥DF,∴DE=EF.
∵DE⊥CF,∴△DEF为等腰直角三角形.
∴∠F=∠FEH=∠HDE=45°.
∵∠P=15°,∴∠DCF=∠P+∠CEP
=15°+45°=60°.
∴∠DOH=60°.
在Rt△ODH中,DH=OD·sin∠DOH=2·sin60°=![]() .
.
在Rt△DHE中,DE=![]() .
.
在Rt△CDE中,∠DCE=60°,
∴EC=DE·cot60°=![]() .
.
∴CF=EF+CE=![]() .
.


科目:高中数学 来源: 题型:
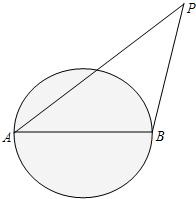 外轮除特许外,不得进入离我国海岸线12海里以内的区域,如图:我国某海岛海岸线是半径为6海里的圆形区域,在直径的两个端点A、B设立两个观察点,已知一外轮在点P处,测得∠BAP=α,∠ABP=β.
外轮除特许外,不得进入离我国海岸线12海里以内的区域,如图:我国某海岛海岸线是半径为6海里的圆形区域,在直径的两个端点A、B设立两个观察点,已知一外轮在点P处,测得∠BAP=α,∠ABP=β.查看答案和解析>>
科目:高中数学 来源: 题型:
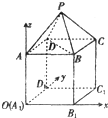 在如图所示的坐标系中,已知P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体.其中AB=2,PA=
在如图所示的坐标系中,已知P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体.其中AB=2,PA=| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
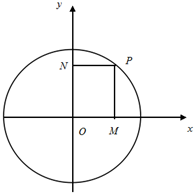 如图,已知P是单位圆(圆心在坐标原点)上一点,∠xOP=
如图,已知P是单位圆(圆心在坐标原点)上一点,∠xOP=| π |
| 3 |
| π |
| 6 |
| π |
| 4 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
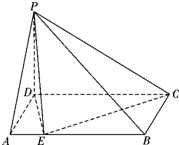 (2012•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点.已知PD=
(2012•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点.已知PD=| 2 |
| 3 |
| π |
| 6 |
2
| ||
| 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com