
【题目】已知点![]() ,圆
,圆![]() ,过点
,过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)当![]() (
(![]() 不重合)时,求
不重合)时,求![]() 的方程及
的方程及![]() 的面积.
的面积.
【答案】(I)![]() ;(II)
;(II)![]() (或
(或![]() ) ,
) , ![]()
【解析】
(Ⅰ)由圆C的方程求出圆心坐标和半径,设出M坐标,由![]() 与
与![]() 数量积等于0列式得M的轨迹方程;
数量积等于0列式得M的轨迹方程;
(Ⅱ)设M的轨迹的圆心为N,由|OP|=|OM|得到ON⊥PM.求出ON所在直线的斜率,由直线方程的点斜式得到PM所在直线方程,由点到直线的距离公式求出O到l的距离,再由弦心距、圆的半径及弦长间的关系求出PM的长度,代入三角形面积公式得答案.
(I)圆C的方程可化为![]() ,∴圆心为
,∴圆心为![]() ,半径为4,设
,半径为4,设![]() ,
,
∴![]() 由题设知
由题设知![]()
![]() ,即
,即![]() .由于点
.由于点![]() 在圆
在圆![]() 的内部,所以
的内部,所以![]() 的轨迹方程是
的轨迹方程是![]() .
.
(II)由(I)可知![]() 的轨迹是以点
的轨迹是以点![]() 为圆心,
为圆心,![]() 为半径的圆.
为半径的圆.
由于![]() ,故
,故![]() 在线段
在线段![]() 的垂直平分线上,又
的垂直平分线上,又![]() 在圆
在圆![]() 上,从而
上,从而![]() .
.
∵![]() 的斜率为3
的斜率为3![]()
![]() ∴
∴![]() 的方程为
的方程为![]() .(或
.(或![]() ).又
).又![]() ,
,![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() ,∴
,∴![]() 的面积为
的面积为![]()


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】国内某知名大学有男生14000人,女生10000人.该校体育学院想了解本校学生的运动状况,根据性别采取分层抽样的方法从全校学生中抽取120人,统计他们平均每天运动的时间(已知该校学生平均每天运动的时间范围是![]()
![]() ),如下表所示.
),如下表所示.
男生平均每天运动的时间分布情况:

女生平均每天运动的时间分布情况:
![]()
(1)假设同组中的每个数据均可用该组区间的中间值代替,请根据样本估算该校男生平均每天运动的时间(结果精确到0.1).
(2)若规定平均每天运动的时间不少于![]() 的学生为“运动达人”,低于
的学生为“运动达人”,低于![]() 的学生为“非运动达人”.
的学生为“非运动达人”.
(ⅰ)根据样本估算该校“运动达人”的数量;
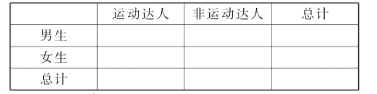
(ⅱ)请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“运动达人”与性别有关.
列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“运动达人”与性别有关.
参考公式:  ,其中
,其中![]() .
.
参考数据:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“珠算之父”程大为是我国明代伟大数学家,他的应用数学巨著《算法统综》的问世,标志着我国的算法由筹算到珠算转变的完成,程大位在《算法统综》中常以诗歌的形式呈现数学问题,其中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上稍四节储三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明”((注)三升九:![]() 升,次第盛;盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为( )
升,次第盛;盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为( )
A.![]() 升B.
升B.![]() 升C.
升C.![]() 升D.
升D.![]() 升
升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)已知等差数列{an}的首项a1≠0,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4.
(1)求证:数列{bn}中的每一项都是数列{an}中的项;
(2)若a1=2,设cn=![]() ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;
(3)在(2)的条件下,若有f(n)=log3Tn,求f(1)+f(2)+…+f(n)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区积极发展电商,通过近些年工作的开展在新农村建设和扶贫过程中起到了非常重要的作用,促进了农民生活富裕,为了更好地了解本地区某一特色产品的宣传费![]() (千元)对销量
(千元)对销量![]() (千件)的影响,统计了近六年的数据如下:
(千件)的影响,统计了近六年的数据如下:

(1)若近6年的宣传费![]() 与销量
与销量![]() 呈线性分布,由前5年数据求线性回归直线方程,并写出
呈线性分布,由前5年数据求线性回归直线方程,并写出![]() 的预测值;
的预测值;
(2)若利润与宣传费的比值不低于20的年份称为“吉祥年”,在这6个年份中任意选2个年份,求这2个年份均为“吉祥年”的概率
附:回归方程![]() 的斜率与截距的最小二乘法估计分别为
的斜率与截距的最小二乘法估计分别为 ,
,
![]() ,其中
,其中![]() ,
, ![]() 为
为![]() ,
, ![]() 的平均数.
的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的图象两相邻对称轴之间的距离是
的图象两相邻对称轴之间的距离是![]() ,若将
,若将![]() 的图象向右平移
的图象向右平移![]() 个单位长度,所得图象对应的函数
个单位长度,所得图象对应的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的对称轴及单调增区间;
的对称轴及单调增区间;
(3)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,是奇函数.
,是奇函数.
(1)求实数m的值;
(2)画出函数![]() 的图象,并根据图象求解下列问题;
的图象,并根据图象求解下列问题;
①写出函数![]() 的值域;
的值域;
②若函数![]() 在区间
在区间![]() 上单调递增,求实数a的取值范围.
上单调递增,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com