
【题目】如图所示,在直角梯形ABCD中,已知![]() ,
,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
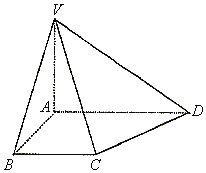
(1)求证:![]() 平面VAC;
平面VAC;
(2)若![]() ,求CV与平面VAD所成角的大小.
,求CV与平面VAD所成角的大小.
【答案】(1)见解析(2)![]()
【解析】
(1)证明连结AC,取AD中点G,连CG,证明四边形ABCG为正方形.推出![]() ,
,![]() ,即可证明
,即可证明![]() 平面VAC.
平面VAC.
(2)连VG,说明![]() 面VAD,
面VAD,![]() 是CV与平面VAD所成的角,通过求解三角形得到CV与平面VAD所成角为
是CV与平面VAD所成的角,通过求解三角形得到CV与平面VAD所成角为![]() .
.
法2:以A为原点,射线AB,AD,AV所在直线为x,y,z轴正半轴,建立空间直角坐标系,平面VAD法向量![]() ,又
,又![]() ,利用空间向量的数量积求解即可.
,利用空间向量的数量积求解即可.
(1)证明:连结AC,∵![]() ,
,![]() ,∴
,∴![]() ,
,
取AD中点G,连CG,
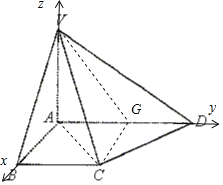
因为![]() ,所以四边形ABCG为正方形.
,所以四边形ABCG为正方形.
所以![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]()
所以![]() ,
,
又![]() 平面ABCD,所以
平面ABCD,所以![]() ,
,
![]() 平面VAC
平面VAC
(2)解:法1:连VG
由![]()
![]()
![]() 面VAD,∴
面VAD,∴![]() 是CV与平面VAD所成的角
是CV与平面VAD所成的角
![]() ;
;![]() ,∴
,∴![]()
∴CV与平面VAD所成角为![]()
法2:以A为原点,射线AB,AD,AV所在直线为x,y,z轴正半轴,建立空间直角坐标系,则平面VAD法向量![]() ,又
,又![]() ,设向量
,设向量![]() 与
与![]() 夹角为
夹角为![]() ,则
,则![]() ,
,![]() ,CV与平面VAD所成的角为
,CV与平面VAD所成的角为![]() .
.


科目:高中数学 来源: 题型:
【题目】某校实行选科走班制度,张毅同学的选择是地理生物政治这三科,且生物在B层班级,该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有__________种
第一节 | 第二节 | 第三节 | 第四节 |
地理1班 | 化学A层3班 | 地理2班 | 化学A层4班 |
生物A层1班 | 化学B层2班 | 生物B层2班 | 历史B层1班 |
物理A层1班 | 生物A层3班 | 物理A层2班 | 生物A层4班 |
物理B层2班 | 生物B层1班 | 物理B层1班 | 物理A层4班 |
政治1班 | 物理A层3班 | 政治2班 | 政治3班 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的准线方程为x=﹣1.
(1)求抛物线C的方程;
(2)过抛物线C的焦点作直线l,交抛物线C于A,B两点,若线段AB中点的横坐标为6,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三上学期期末数学考试成绩中,随机抽取了![]() 名学生的成绩得到如图所示的频率分布直方图:
名学生的成绩得到如图所示的频率分布直方图:
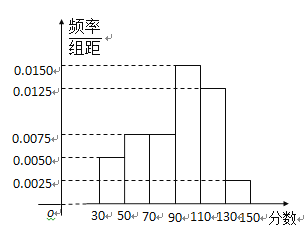
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在![]() 和
和![]() 的学生中共抽取
的学生中共抽取![]() 人,该
人,该![]() 人中成绩在
人中成绩在![]() 的有几人?
的有几人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求分数在
人,求分数在![]() 和
和![]() 各
各![]() 人的概率.
人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 与
与![]() 均为菱形,
均为菱形,![]() ,且
,且![]() .
.
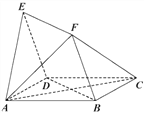
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若![]() 为线段
为线段![]() 上的一点,且满足直线
上的一点,且满足直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点F的距离为5.
到其焦点F的距离为5.
(1)求抛物线C的方程;
(2)设直线l与抛物线C交于A、B两点,O为坐标原点,若![]() ,求证:直线l必过一定点,并求出该定点的坐标;
,求证:直线l必过一定点,并求出该定点的坐标;
(3)过点![]() 的直线m与抛物线C交于不同的两点M、N,若
的直线m与抛物线C交于不同的两点M、N,若![]() ,求直线m的斜率的取值范围.
,求直线m的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是 ![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() .
.
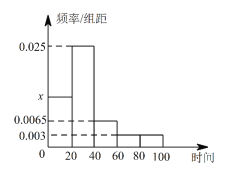
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)如果年上缴税收不少于![]() 万元的企业可申请政策优惠,若共抽取企业
万元的企业可申请政策优惠,若共抽取企业![]() 个,试估计有多少企业可以申请政策优惠;
个,试估计有多少企业可以申请政策优惠;
(Ⅲ)从企业中任选![]() 个,这
个,这![]() 个企业年上缴税收少于
个企业年上缴税收少于![]() 万元的个数记为
万元的个数记为 ![]() ,求
,求![]() 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将![]() 沿AB折到
沿AB折到![]() 的位置,使
的位置,使![]() ,点E在SD上,且
,点E在SD上,且![]() ,如下图。
,如下图。
(1)求证: ![]() 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.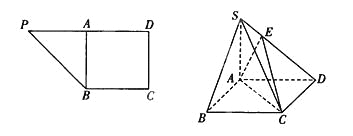
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com