
如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
箱子底边长取40 cm时,容积最大,最大容积为16 000 cm3.
【解析】
试题分析:设箱子的底边长为x
cm,则箱子高h= cm.
cm.
箱子容积V=V(x)=x2h= (0<x<60).
(0<x<60).
求V(x)的导数,得V′(x)=60x-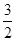 x2=0,
x2=0,
解得x1=0(不合题意,舍去),x2=40.
当x在(0,60)内变化时,导数V′(x)的正负如下表:
|
x |
(0,40) |
40 |
(40,60) |
|
V′(x) |
+ |
0 |
- |
因此在x=40处,函数V(x)取得极大值,并且这个极大值就是函数V(x)的最大值.
将x=40代入V(x)
得最大容积V=402× =16 000(cm3).
=16 000(cm3).
所以箱子底边长取40 cm时,容积最大,最大容积为16 000 cm3.
考点:本题主要考查函数模型,应用导数研究函数的单调性、最值。
点评:典型题,本题属于函数及导数应用中的基本问题,通过研究构建函数函数模型,利用导数求函数的最值。关于函数应用问题的考查,在高考题中往往是“一大两小”。构建函数模型的步骤“审清题意、设出变量、确定函数、求解答案、写出结语”。本题利用均值定理,确定函数的最值。


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
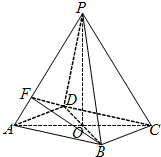 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=| 6 |
| BM |
| BP |
查看答案和解析>>
科目:高中数学 来源:单元双测 同步达标活页试卷 高二数学(下A) 人教版 题型:013
如图所示,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF=![]() ,EF与面AC的距离为2,则该多面体的体积为
,EF与面AC的距离为2,则该多面体的体积为

A.![]()
B.5
C.6
D.![]()
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
如图所示,在多面体ABCDEF中,已知ABCD是边长为3的正方形,EF∥AB, ,EF与面AC的距离为2,则该多面体的体积为
,EF与面AC的距离为2,则该多面体的体积为

[ ]


查看答案和解析>>
科目:高中数学 来源: 题型:013
如图所示,在多面体
ABCDEF中,已知ABCD是边长为3的正方形,EF∥AB, ,EF与面AC的距离为2,则该多面体的体积为
,EF与面AC的距离为2,则该多面体的体积为

[
]|
A . |
B .5 |
C .6 |
D . |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省郴州市高三下学期第六次月考理科数学 题型:解答题
(本小题满分13分)
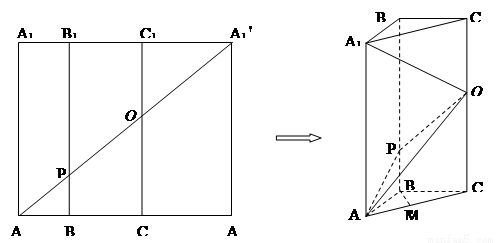
如图5所示 :在边长为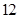 的正方形
的正方形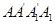 中,
中,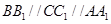 ,且
,且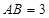 ,
,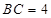 ,
,
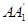 分别交
分别交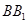 、
、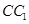 于
于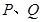 两点, 将正方形沿
两点, 将正方形沿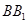 、
、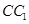 折叠,使得
折叠,使得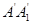 与
与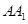 重合,
重合,
构成如图6所示的三棱柱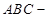
 .
.
( I )在底边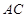 上有一点
上有一点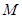 ,且
,且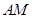 :
: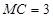 :
: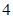 ,
求证:
,
求证: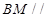 平面
平面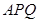 ;
;
( II )求直线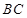 与平面
与平面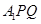 所成角的正弦值
所成角的正弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com