
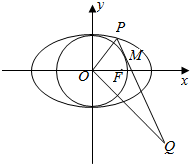
 在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.
在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.分析 (1)运用椭圆的离心率公式和a,b,c的关系,解方程可得a,b,进而得到椭圆的方程;
(2)设P(x0,y0),运用两点的距离公式和焦半径公式,结合椭圆的范围,即可得到所求范围;
(3)方法一、讨论当PM⊥x轴时,当PM不垂直于x轴时,设出直线方程,联立椭圆方程,运用向量垂直的条件:数量积为0,计算即可得到所求值;
方法二、设P(x0,y0),则直线OQ:$y=-\frac{x_0}{y_0}x$,求得$Q(-\frac{y_0}{x_0}t,t)$,由OP⊥OQ,可得OP•OQ=OM•PQ,再由两点的距离公式,化简整理即可得到所求值.
解答 解:(1)由题意可得$\left\{\begin{array}{l}\frac{c}{a}=\frac{1}{2}\\ c=1\end{array}\right.$,
∴c=1,a=2,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
∴椭圆方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)设P(x0,y0),则$\frac{{{x_0}^2}}{4}+\frac{{{y_0}^2}}{3}=1(0<{x_0}<2)$,
PM=$\sqrt{{x_0}^2+{y_0}^2-3}=\sqrt{{x_0}^2+3-\frac{3}{4}{x_0}^2-3}=\frac{1}{2}{x_0}$,
PF=$2-\frac{1}{2}{x_0}$,∴PM•PF=$\frac{1}{4}{x_0}(4-{x_0})=-\frac{1}{4}{({x_0}-2)^2}+1$,
∵0<x0<2,
∴|PM|•|PF|的取值范围是(0,1);
(3)法一:①当PM⊥x轴时,P$(\sqrt{3},\frac{{\sqrt{3}}}{2})$,Q$(\sqrt{3},t)$或$(-\sqrt{3},t)$,
由$\overrightarrow{OP}•\overrightarrow{OQ}=0$,解得$t=±2\sqrt{3}$;
②当PM不垂直于x轴时,设P(x0,y0),PQ方程为y-y0=k(x-x0),
即kx-y-kx0+y0=0,
∵PQ与圆O相切,∴$\frac{{|k{x_0}-{y_0}|}}{{\sqrt{{k^2}+1}}}=\sqrt{3}$,
∴${(k{x_0}-{y_0})^2}=3{k^2}+3$
∴2kx0y0=${k^2}{x_0}^2+{y_0}^2-3{k^2}-3$,
又$Q(\frac{{t-{y_0}+k{x_0}}}{k},t)$,
所以由$\overrightarrow{OP}•\overrightarrow{OQ}=0$得$t=\frac{{{x_0}({y_0}-k{x_0})}}{{{x_0}+k{y_0}}}$,
∴${t^2}=\frac{{{x_0}^2{{({y_0}-k{x_0})}^2}}}{{{{({x_0}+k{y_0})}^2}}}$=$\frac{{{x_0}^2{{(k{x_0}-{y_0})}^2}}}{{{x_0}^2+{k^2}{y_0}^2+2k{x_0}{y_0}}}$
=$\frac{{{x_0}^2(3{k^2}+3)}}{{{x_0}^2+{k^2}{y_0}^2+{k^2}{x_0}^2+{y_0}^2-3{k^2}-3}}$
=$\frac{{{x_0}^2(3{k^2}+3)}}{{(1+{k^2}){x_0}^2+(1+{k^2})(3-\frac{3}{4}{x_0}^2)-3{k^2}-3}}$=12,
∴$t=±2\sqrt{3}$,
综上可得,t=±2$\sqrt{3}$.
法二:设P(x0,y0),则直线OQ:$y=-\frac{x_0}{y_0}x$,∴$Q(-\frac{y_0}{x_0}t,t)$,
∵OP⊥OQ,∴OP•OQ=OM•PQ,
∴$\sqrt{{x_0}^2+{y_0}^2}•\sqrt{\frac{{{y_0}^2}}{{{x_0}^2}}{t^2}+{t^2}}=\sqrt{3}•\sqrt{{{({x_0}+\frac{y_0}{x_0}t)}^2}+({y_0}-t}{)^2}$,
∴$\sqrt{{x_0}^2+{y_0}^2}•\sqrt{\frac{t^2}{{{x_0}^2}}({x_0}^2+{y_0}^2)}=\sqrt{3}•\sqrt{{x_0}^2+\frac{{{y_0}^2}}{{{x_0}^2}}{t^2}+{y_0}^2+{t^2}}=\sqrt{3}•\sqrt{\frac{{{x_0}^2+{y_0}^2}}{{{x_0}^2}}({x_0}^2+{t^2})}$
∴$({x_0}^2+{y_0}^2){t^2}=3({x_0}^2+{t^2})$,∴${t^2}=\frac{{3{x_0}^2}}{{{x_0}^2+{y_0}^2-3}}$,
∵$\frac{{{x_0}^2}}{4}+\frac{{{y_0}^2}}{3}=1$,∴${y_0}^2=3-\frac{{3{x_0}^2}}{4}$,∴${t^2}=\frac{{3{x_0}^2}}{{\frac{1}{4}{x_0}^2}}=12$,
∴$t=±2\sqrt{3}$.
点评 本题考查椭圆的方程的求法,注意运用椭圆的离心率公式,考查椭圆的焦半径公式和椭圆的范围,同时考查向量垂直的条件,考查化简整理的运算求解的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{OM}$=2$\overrightarrow{OA}$-$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{OM}$+$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$ | ||
| C. | $\overrightarrow{OM}$=$\frac{1}{5}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$ | D. | $\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=$\overrightarrow{0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ksin(π+α)>0 | B. | kcos(π-α)>0 | C. | ksinα≤0 | D. | kcosα≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
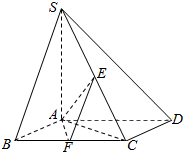 如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.
如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$+$\frac{\sqrt{2}}{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | 1+$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
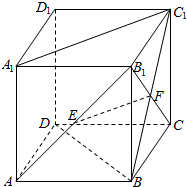
| A. | EF与BB1垂直 | B. | EF与BD垂直 | C. | EF与CD异面 | D. | EF与A1C1异面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com