
分析 先利用周期性将$f({-\frac{14π}{3}})$化成定义在区间(-$\frac{π}{2}$,0)上的函数值为f(-$\frac{π}{6}$)再代入解析式计算求解.
解答 解:$f({-\frac{14π}{3}})$=f(-$\frac{14π}{3}+3×\frac{3π}{2}$)=f(-$\frac{π}{6}$),
由于-$\frac{π}{2}$<-$\frac{π}{6}$<0,
所以$f({-\frac{14π}{3}})$=f(-$\frac{π}{6}$)=cos(-$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查分段函数求函数值,考查转化、计算、分类能力,属于基础题.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{7}{4}$,+∞) | B. | (一∞,$\frac{7}{4}$) | C. | (0,$\frac{7}{4}$) | D. | ($\frac{7}{4}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-2,$\frac{9}{4}$) | C. | (-$\frac{9}{4}$,$\frac{9}{4}$) | D. | $(-\frac{9}{4},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
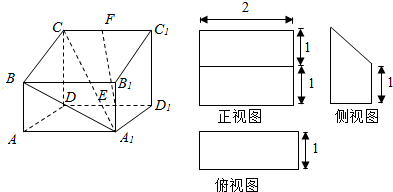 四棱柱ABCD-A1B1C1D1的三视图如图所示,E、F分别为A1B1、CC1的中点.
四棱柱ABCD-A1B1C1D1的三视图如图所示,E、F分别为A1B1、CC1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com