Question

（2013•丽水一模）已知直三棱柱ABC-A₁B₁C₁，底面△ABC是等腰三角形，∠BAC=120°，AB=

1

2

AA1=4，CN=3AN，点M，P，Q分别是AA₁，A₁B₁，BC的中点．
（Ⅰ）求证：直线PQ∥平面BMN；
（Ⅱ）求直线AB与平面BMC所成角的正弦值．

Answer 1

分析：（Ⅰ）要证明直线PQ∥平面BMN，可在平面BMN中找到一条与PQ平行的直线即可，根据题目给出的P，Q分别是A₁B₁，BC的中点，想到取AB的中点G，连接PG，QG后分别交BM，BN于点E，F，根据题目给出的线段的长及线段之间的关系证出

GE

EP

=

GF

FQ

=

1

3

，从而得到EF∥PQ，然后利用线面平行的判定即可得证；
（Ⅱ）求直线AB与平面BMC所成角的正弦值，首先是找角，由题意能够得到平面BMC⊥平面AMQ，所以直接过A作MQ的垂线
AO，连接BO，在直角三角形AOB中求解∠BAO的正弦值．

解答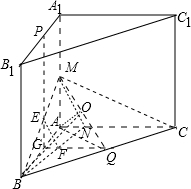：（Ⅰ）证明：如图，
取AB中点G，连结PG，QG分别交BM，BN于点E，F，
则E，F分别为BM，BN的中点．
而GE∥

1

2

AM，GE=

1

2

AM，GF∥

1

2

AN，GF=

1

2

AN．
且CN=3AN，所以 

GE

EP

=

1

3

，

GF

FQ

=

AN

NC

=

1

3

，
所以

GE

EP

=

GF

FQ

=

1

3

．
所以 EF∥PQ，又 EF?平面BMN，PQ?平面BMN．
所以 PQ∥平面BMN；
（Ⅱ）解：连接AQ，∵△ABC是等腰三角形，Q是BC的中点，∴AQ⊥BC，连接MQ，
作AO⊥MQ于O，连接BO，∵MA⊥平面ABC，∴MA⊥BC，
又AQ⊥BC，∴BC⊥平面AQM，∴BC⊥AO．
∵AO⊥MQ，∴AO⊥平面BCM，∴∠ABO就是AB与平面ABC所成在角．
在Rt△AQC中，∵∠QAC=60°，∴AQ=2．
在△RtAQM中，∵MQ=2

5

，由AM•AQ=MQ•AO，得AO=

AM•AQ

MQ

=

4×2

2 5

=

4 5

5

，
所以sin∠ABO=

AO

AB

=

5

5

．

点评：本题考查了直线与平面平行的判定，考查了线面角，证明线面平行时，常借助于三角形的中位线得线线平行，求线面角时，关键是把找出的角能够放在一个易于求解的三角形当中，此题是中档题．