
【题目】已知函数![]() ,
, ![]() ,
, ![]() .
.
(1)设函数![]() ,若
,若![]() 在区间
在区间![]() 上单调,求实数
上单调,求实数![]() 的取值范围;
的取值范围;
(2)求证: ![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,且a3=﹣6,a6=0.
(1)求{an}的通项公式.
(2)若等比数列{bn}满足b1=8,b2=a1+a2+a3 , 求{bn}的前n项和公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医生的专业能力参数![]() 可有效衡量医生的综合能力,
可有效衡量医生的综合能力,![]() 越大,综合能力越强,并规定: 能力参数
越大,综合能力越强,并规定: 能力参数![]() 不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力
不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力![]() 的频率分布直方图:
的频率分布直方图:
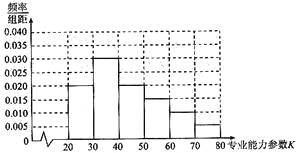
(Ⅰ)求出这个样本的合格率、优秀率;
(Ⅱ)现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名.
①求这2名医生的能力参数![]() 为同一组的概率;
为同一组的概率;
②设这2名医生中能力参数![]() 为优秀的人数为
为优秀的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生小王自主创业,在乡下承包了一块耕地种植某种水果,每季投入2万元,根据以往的经验,每季收获的此种水果能全部售完,且水果的市场价格和这块地上的产量具有随机性,互不影响,具体情况如表:

(Ⅰ)设![]() 表示在这块地种植此水果一季的利润,求
表示在这块地种植此水果一季的利润,求![]() 的分布列及期望;
的分布列及期望;
(Ⅱ)在销售收入超过5万元的情况下,利润超过5万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ![]() =
= 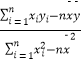 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,
,
参考数据:7×165+6×142+6×148+5×125+6×150=4420.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为梯形,
为梯形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
?若有,请找出具体位置,并进行证明:若无,请分析说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的空间几何体中,底面四边形![]() 为正方形,
为正方形, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
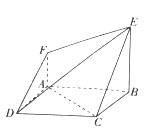
(1)求二面角![]() 的大小;
的大小;
(2)若在平面![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,试通过计算说明点
,试通过计算说明点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
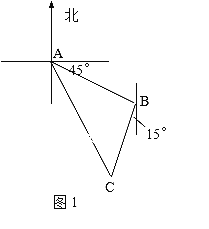
【题目】如图1,甲船在A处,乙船在A处的南偏东45°方向,距A有9n mile并以20n mile/h的速度沿南偏西15°方向航行,若甲船以28n mile/h的速度航行,应沿什么方向,用多少h能尽快追上乙船?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料,生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示:
| A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车品乙种肥料,产生的利润为3万元、分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料,求出此最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com