
如图,四棱锥 中,底面
中,底面 为梯形,
为梯形,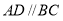 ,
, ,
, ,平面
,平面 平面
平面 ,
, .
.

(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)是否存在点 ,到四棱锥
,到四棱锥 各顶点的距离都相等?并说明理由.
各顶点的距离都相等?并说明理由.
(1)参考解析;(2)参考解析;(3)存在
【解析】
试题分析:(1)线面平面平行的证明,关键是在平面内找到一条直线与要证明的直线平行,根据 ,再根据直线BC,直线AD的位置关系,即可得线面平行.线面平行还有一种就是转化为面面平行.线面平行的证明就是这两种判断的相互转化.
,再根据直线BC,直线AD的位置关系,即可得线面平行.线面平行还有一种就是转化为面面平行.线面平行的证明就是这两种判断的相互转化.
(2)要证线线垂直转化为线面垂直,由题意可知,通过证明直线AC垂直于平面PAB,由面面垂直可知,只需证明直线AC垂直于AB,在三角形ABC中,由所给条件即可得到AC垂直于AB.
(3)由(2)可知直线PB垂直于平面PAC.所以可得直线PB垂直于直线PC.通过三角形的BCD全等于三角形CBA,所以可得直线BD垂直于DC.所以BC是 的斜边,即BC的中点就是所要找的Q点.
的斜边,即BC的中点就是所要找的Q点.
试题解析:(1)证明:底面 为梯形,
为梯形, ,
,
又 平面
平面 ,
, 平面
平面 ,
,
所以 平面
平面 .
.
(2)证明:设 的中点为
的中点为 ,连结
,连结 ,在梯形
,在梯形 中,
中,

因为  ,
, ,
,
所以  为等边三角形,
为等边三角形, ,
,
又  ,
,
所以 四边形 为菱形.
为菱形.
因为 ,
,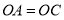 ,
,
所以 ,
,
所以 ,
, ,
,
又平面 平面
平面 ,
, 是交线,
是交线,
所以  平面
平面 ,
,
所以  ,即
,即 .
.
(3)【解析】
因为  ,
, ,所以
,所以 平面
平面 .
.
所以, ,
,
所以  为直角三角形,
为直角三角形, .
.
连结 ,由(2)知
,由(2)知 ,
,
所以  ,
,
所以  为直角三角形,
为直角三角形, .
.
所以点 是三个直角三角形:
是三个直角三角形: 、
、 和
和 的共同的斜边
的共同的斜边 的中点,
的中点,
所以  ,
,
所以存在点 (即点
(即点 )到四棱锥
)到四棱锥 各顶点的距离都相等.
各顶点的距离都相等.
考点:1.线面平行的判定.2.线线垂直的判定.3.直角三形的性质.4.归纳推理论证的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届吉林省吉林市高二上学期期末文数学试卷(解析版) 题型:选择题
双曲线 的左、右焦点分别是
的左、右焦点分别是 ,过
,过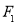 作倾斜角为
作倾斜角为 的直线交双曲线右支于
的直线交双曲线右支于 点,若
点,若 垂直于
垂直于 轴,则双曲线的离心率为
轴,则双曲线的离心率为
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届北京海淀区高二上学期期末考试文科数学试卷(解析版) 题型:选择题
已知命题 函数
函数 是增函数,命题
是增函数,命题
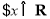 ,
, 的导数大于0,那么 ( )
的导数大于0,那么 ( )
(A) 是真命题 (B)
是真命题 (B) 是假命题
是假命题
(C) 是真命题 (D)
是真命题 (D) 是真命题
是真命题
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二第一学期期末文科数学试卷(解析版) 题型:填空题
已知正方体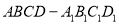 ,点
,点 、
、 、
、 分别是棱
分别是棱 、
、 和
和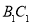 上的动点,观察直线
上的动点,观察直线 与
与 ,
, 与
与 .
.

给出下列结论:
①对于任意点 ,存在点
,存在点 ,使得
,使得
 ;②对于任意点
;②对于任意点 ,存在点
,存在点 ,使得
,使得
 ;
;
③对于任意点 ,存在点
,存在点 ,使得
,使得
 ;④对于任意点
;④对于任意点 ,存在点
,存在点 ,使得
,使得
 .
.
其中,所有正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
已知抛物线 的准线与双曲线
的准线与双曲线  交于
交于 ,
, 两点,点
两点,点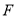 为抛物线的焦点,若△
为抛物线的焦点,若△ 为直角三角形,则
为直角三角形,则 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com