
如图,某城市有一块半径为40 m的半圆形绿化区域(以O 为圆心,AB为直径),现计划对其进行改建.在AB的延长线上取点D,OD=80 m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2.设∠AOC=x rad.

(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)试问∠AOC多大时,改建后的绿化区域面积S取得最大值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2017届福建连城县朋口中学高三上期中数学(理)试卷(解析版) 题型:选择题
设集合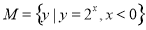 ,
,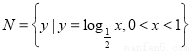 ,则“
,则“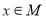 ”是“
”是“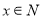 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2017届江苏南通中学高三上期中数学(理)试卷(解析版) 题型:解答题
已知曲线C的极坐标方程为 ?=2cosθ,直线l的极坐标方程为 ? sin(θ+ )=m.若直线l与曲线C有且只有一个公共点,求实数m的值.
)=m.若直线l与曲线C有且只有一个公共点,求实数m的值.
查看答案和解析>>
科目:高中数学 来源:2017届江苏南通中学高三上期中数学(理)试卷(解析版) 题型:填空题
已知 为数列
为数列 的前
的前 项和,
项和, ,
, ,若关于正整数
,若关于正整数 的不等式
的不等式 的解集中的整数解有两个,则正实数
的解集中的整数解有两个,则正实数 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:2017届广东韶关市六校高三10月联考数学(文)试卷(解析版) 题型:解答题
某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间 ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com