
 -x1) (
-x1) ( -x2)≥(
-x2)≥( -
- )2恒成立的k的取值范围.
)2恒成立的k的取值范围.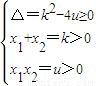 …(3分)解得0<u≤
…(3分)解得0<u≤ ,
,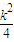 ];…(6分)
];…(6分) -x1) (
-x1) (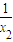 -x2)=x1x2+
-x2)=x1x2+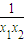 -
-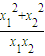 =u-
=u-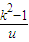 +2.
+2.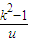 +2(u>0),所以f′(u)=1+
+2(u>0),所以f′(u)=1+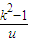 ,…(8分)
,…(8分)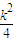 ,所以f′(u)>0,从而f (u)在(0,
,所以f′(u)>0,从而f (u)在(0,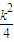 ]为增函数,所以
]为增函数,所以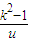 +2≤f (
+2≤f (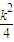 )=
)=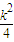 -
-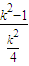 +2=(
+2=(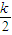 -(
-(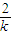 )2,
)2,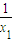 -x1) (
-x1) (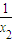 -x2)≥((
-x2)≥((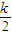 -(
-(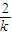 )2不恒成立.…(10分)
)2不恒成立.…(10分)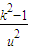 =0,得u=
=0,得u=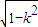 ,
,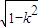 ),f′(u)<0;当u∈(
),f′(u)<0;当u∈(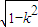 ,+∞),f′(u)>0,
,+∞),f′(u)>0,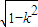 ]上递减,在[
]上递减,在[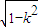 ,+∞)上递增,…(12分)
,+∞)上递增,…(12分)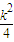 ]上恒有f (u)≥f (
]上恒有f (u)≥f (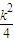 ),必有
),必有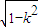 ≥
≥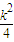 ,即k4+16 k2-16≤0,…(14分)
,即k4+16 k2-16≤0,…(14分)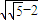 .综上,k的取值范围是(0,2
.综上,k的取值范围是(0,2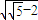 ].…(16分)
].…(16分)

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省鄂州市高三期中考试文科数学 题型:填空题
以下四个关于圆锥曲线的命题中:
①设A、B为两个定点,k为正常数,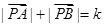 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;
②双曲线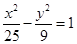 与椭圆
与椭圆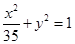 有相同的焦点;
有相同的焦点;
③方程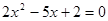 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④已知点P(x,y)的坐标满足方程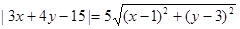 ,则点P的轨迹是一条直线.
,则点P的轨迹是一条直线.
其中真命题的序号为 _______.
查看答案和解析>>
科目:高中数学 来源:南京模拟 题型:解答题
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com