
 如图,一个8×8的国际象棋盘有32个黑格和32个白格.一条“线路”由8个白格组成,每行有一个,且相邻的白格有公共顶点,则这样的“路线”共有________条(请用数字作答)
如图,一个8×8的国际象棋盘有32个黑格和32个白格.一条“线路”由8个白格组成,每行有一个,且相邻的白格有公共顶点,则这样的“路线”共有________条(请用数字作答)
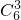 =20条;
=20条;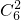 =15条;
=15条;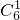 =6条;
=6条;

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:单选题
 如图,正方体ABCD-A′B′C′D′中,M、E是AB的三等分点,G、N是CD的三等分点,F、H分别是BC、MN的中点,则四棱锥A′-EFGH的侧视图为
如图,正方体ABCD-A′B′C′D′中,M、E是AB的三等分点,G、N是CD的三等分点,F、H分别是BC、MN的中点,则四棱锥A′-EFGH的侧视图为



查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个 数 | 20 | 30 | 80 | 40 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com