Question

【题目】已知中心在原点，焦点在轴上，离心率为的椭圆过点.

（1）求椭圆方程；

（2）设不过原点O的直线，与该椭圆交于P、Q两点，直线OP、OQ的斜率依次为，满足，求的值.

Answer 1

【答案】（1）；（2）

【解析】

(1)根据题意列出方程组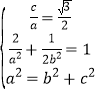：解出即可；（2）联立直线和椭圆得到方程：(4k2＋1)x2＋8kmx＋4m2－4＝0，4k＝k1＋k2＝，由韦达定理得到表达式，进而得到结果.

(1)设椭圆的方程为＋＝1(a>b>0)，则由题意得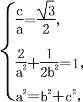解得a＝2，b＝1，

∴椭圆的方程为＋y2＝1.

(2)由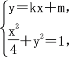得(4k2＋1)x2＋8kmx＋4m2－4＝0，

令Δ＝64k2m2－4(4k2＋1)(4m2－4)>0，得m2<4k2＋1(*)，

∴x1＋x2＝－，x1x2＝，

设P(x1，y1)，Q(x2，y2)，∴k1＝，k2＝，

则4k＝k1＋k2＝＋＝＝＝2k－，

∴m2＝，满足(*)式，故m2＝.