
【题目】2016年1月1日,我国全面实行二孩政策,某机构进行了街头调查,在所有参与调查的青年男女中,持“响应”“犹豫”和“不响应”态度的人数如表所示:
响应 | 犹豫 | 不响应 | |
男性青年 | 500 | 300 | 200 |
女性青年 | 300 | 200 | 300 |
(1)根据已知条件完成下面的2×2列联表,并判断能否有97.5%的把握认为犹豫与否与性别有关;
犹豫 | 不犹豫 | 总计 | |
男性青年 |
|
|
|
女性青年 |
|
|
|
总计 |
|
| 1800 |
(2)以表中频率作为概率,若从街头随机采访青年男女各2人,求4人中“响应”的人数恰好是“不响应”的人数(“不响应”的人数不为0)的2倍的概率.
参考公式: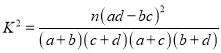
参考数据:
P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)见解析,有97.5%的把握认为犹豫与否与性别有关.(2)![]() .
.
【解析】
(1)直接利用![]() 联图,利用独立性检验求出结果;(2)利用概率知识和排列组合知识的运用求出结果.
联图,利用独立性检验求出结果;(2)利用概率知识和排列组合知识的运用求出结果.
(1)
犹豫 | 不犹豫 | 总计 | |
男性青年 | 300 | 700 | 1000 |
女性青年 | 200 | 600 | 800 |
总计 | 500 | 1300 | 1800 |
所以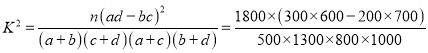
![]() 5.538>5.024,
5.538>5.024,
则有97.5%的把握认为犹豫与否与性别有关.
(2)男性青年中持“响应”“犹豫”“不响应”态度的概率为![]() ,
,![]() ,
,![]() .
.
女性青年中持“响应”“犹豫”“不响应”态度的概率为![]() ,
,![]() ,
,![]() .
.
因为选出的4人中“响应”的人数恰好是“不响应”人数的2倍.
所以响应的人数为2,不响应的人数为1,犹豫的人数为1,
所以所求的概率为P![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面 ABCD为矩形,侧面为正三角形,且平面
中,底面 ABCD为矩形,侧面为正三角形,且平面![]() 平面
平面 ![]() E 为 PD 中点,AD=2.
E 为 PD 中点,AD=2.
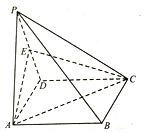
(1)证明平面AEC丄平面PCD;
(2)若二面角![]() 的平面角
的平面角![]() 满足
满足![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别是DD1,DB的中点,G在棱CD上,且CG![]() CD.
CD.
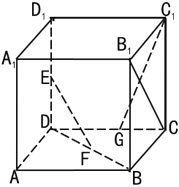
(1)证明:EF⊥B1C;
(2)求cos![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面![]() ,直线
,直线![]() .给出下列命题:
.给出下列命题:
① 若![]() ,则
,则![]() ; ② 若
; ② 若![]() ,则
,则![]() ;
;
③ 若![]() ,则
,则![]() ; ④ 若
; ④ 若![]() ,则
,则![]() .
.
其中是真命题的是_________.(填写所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道(![]() )和唯众传媒联合制作的《开讲啦》是中国首档青春电视公开课。每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
)和唯众传媒联合制作的《开讲啦》是中国首档青春电视公开课。每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表:
列联表:
非常满意 | 满意 | 合计 | |
| 30 |
| |
|
|
| |
合计 |
已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为
地区当中“非常满意”的观众的概率为![]() ,且
,且![]() .
.
(Ⅰ)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“满意”的![]() 、
、![]() 地区的人数各是多少;
地区的人数各是多少;
(Ⅱ)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系;
的把握认为观众的满意程度与所在地区有关系;
(Ⅲ)若以抽样调查的频率为概率,从![]() 地区随机抽取3人,设抽到的观众“非常满意”的人数为
地区随机抽取3人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
|
|
|
|
|
|
|
|
|
|
附:参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在平面直角坐标系的原点![]() 处,极轴与
处,极轴与![]() 轴的非负半轴重合,且长度单位相同,直线
轴的非负半轴重合,且长度单位相同,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() (
(![]() 为参数).其中
为参数).其中![]() .
.
(1)试写出直线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的普通方程;
的普通方程;
(2)若点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
(1)当a=b=1时,求函数f(x)的图象在点(e2,f(e2))处的切线方程;
(2)当b=1时,若存在![]() ,使f(x1)≤f'(x2)+a成立,求实数a的最小值.
,使f(x1)≤f'(x2)+a成立,求实数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() ,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若
,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若![]() OMN为直角三角形,则|MN|=
OMN为直角三角形,则|MN|=
A. ![]() B. 3 C.
B. 3 C. ![]() D. 4
D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com