
【题目】某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 | [160,165) | 5 | 0.050 |
第2组 | [165,170) | n | 0.350 |
第3组 | [170,175) | 30 | p |
第4组 | [175,180) | 20 | 0.200 |
第5组 | [180,185] | 10 | 0.100 |
合计 | 100 | 1.000 |
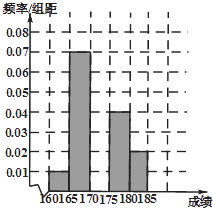
(1)求频率分布表中n,p的值,并补充完整相应的频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.
【答案】
(1)解:由题意可知,第2组的频数n=0.35×100=35人,
第3组的频率p= ![]() ,
,
(2)解:∵第3、4、5组共有60名学生,
∴利用分层抽样在60名学生中抽取6名学生,
每组分别为:第3组: ![]() ×6=3人,第4组:
×6=3人,第4组: ![]() ×6=2人,第5组:
×6=2人,第5组: ![]() =1人,
=1人,
∴第3、4、5组分别抽取3人、2人、1人
(3)解:试验发生包含的事件是从六位同学中抽两位同学有C62=15种
满足条件的事件是第4组至少有一名学生被考官A面试有C21C41+1=9种结果,
∴至少有一位同学入选的概率为 ![]() =
= ![]()
【解析】(1)根据所给的第二组的频率,利用频率乘以样本容量,得到要求的频数,再根据所给的频数,利用频除以样本容量,得到要求的频率.(2)因为在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生,而这三个小组共有60人,利用每一个小组在60人中所占的比例,乘以要抽取的人数,得到结果.(3)试验发生包含的事件是从六位同学中抽两位同学有C62种满足条件的事件是第4组至少有一名学生被考官A面试有C21C41+1种结果,根据古典概型概率公式得到结果.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>2,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个无穷数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,对任意的
,对任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 为等差数列,对任意的
为等差数列,对任意的![]() ,都有
,都有![]() .证明:
.证明: ![]() ;
;
(3)若![]() 为等比数列,
为等比数列, ![]() ,
, ![]() ,求满足
,求满足![]()
![]() 的
的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ),在以坐标原点为极点,
),在以坐标原点为极点, ![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(1)试将曲线![]() 与
与![]() 化为直角坐标系
化为直角坐标系![]() 中的普通方程,并指出两曲线有公共点时
中的普通方程,并指出两曲线有公共点时![]() 的取值范围;
的取值范围;
(2)当![]() 时,两曲线相交于
时,两曲线相交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥A﹣BCD的各个棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( ) 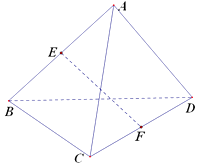
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如表:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)求出y关于x的线性回归方程 ![]() ;
;
(2)试预测加工10个零件需要多少小时?
(参考公式: ![]() =
= 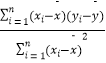 =
= 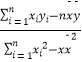 ;
; ![]() ;)
;)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点. 
(1)证明:MN∥平面PAD;
(2)若PB与平面ABCD所成的角为45°,求三棱锥C﹣BDN的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组: ![]() 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。

(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com