
【题目】已知函数f(x)=(x﹣2)ex﹣![]() +
+![]() x,其中
x,其中![]() ∈R,e是自然对数的底数.
∈R,e是自然对数的底数.
(1)当![]() >0时,讨论函数f(x)在(1,+∞)上的单调性;
>0时,讨论函数f(x)在(1,+∞)上的单调性;
(2)若函数g(x)=f![]() (x)+2﹣
(x)+2﹣![]() ,证明:使g(x)≥0在
,证明:使g(x)≥0在![]() 上恒成立的实数a能取到的最大整数值为1.
上恒成立的实数a能取到的最大整数值为1.
【答案】(1)见解析;(2)见解析
【解析】
(1)讨论![]() 的范围,判断f
的范围,判断f![]() (x)的符号,得出f(x)的单调性;
(x)的符号,得出f(x)的单调性;
(2)分别计算![]() =1和
=1和![]() =2时g(x)的最小值,判断g(x)的最小值的符号得出结论.
=2时g(x)的最小值,判断g(x)的最小值的符号得出结论.
(1)f![]() (x)=ex+(x﹣2)ex﹣
(x)=ex+(x﹣2)ex﹣![]() x+
x+![]() =(x﹣1)(ex﹣
=(x﹣1)(ex﹣![]() ),令f
),令f![]() (x)=0解得x=ln
(x)=0解得x=ln![]() ,
,
①若ln![]() ≤1,即0<
≤1,即0<![]() ≤e,则f
≤e,则f![]() (x)≥0在(1,+∞)上恒成立,∴f(x)在(1,+∞)上单调递增;
(x)≥0在(1,+∞)上恒成立,∴f(x)在(1,+∞)上单调递增;
②若ln![]() >1,即
>1,即![]() >e,则当1<x<ln
>e,则当1<x<ln![]() 时,f′(x)<0,当x>ln
时,f′(x)<0,当x>ln![]() 时,f
时,f![]() (x)>0,
(x)>0,
∴f(x)在(1,ln![]() )上单调递减,在(ln
)上单调递减,在(ln![]() ,+∞)上单调递增,
,+∞)上单调递增,
(2)g(x)=ex+(x﹣2)ex﹣![]() x+2,
x+2,
①当![]() =1时,g(x)=ex+(x﹣2)ex﹣x+2,
=1时,g(x)=ex+(x﹣2)ex﹣x+2,![]() =xex﹣1,
=xex﹣1,![]() =(x+1)ex,
=(x+1)ex,
∴当x<﹣1时,![]() <0,当x>﹣1时,
<0,当x>﹣1时,![]() >0,
>0,
∴![]() 在(﹣∞,﹣1)上单调递减,在(﹣1,+∞)上单调递增,
在(﹣∞,﹣1)上单调递减,在(﹣1,+∞)上单调递增,
∴![]() 的最小值为g
的最小值为g![]() (﹣1)=﹣
(﹣1)=﹣![]() ﹣1<0,
﹣1<0,
又当x<0时,![]() <0,g
<0,g![]() (0)=﹣1,g
(0)=﹣1,g![]() (ln2)=2ln2﹣1>0,
(ln2)=2ln2﹣1>0,
∴存在唯一一个实数x0∈(0,ln2),使得g![]() (x0)=0,即x0
(x0)=0,即x0![]() =1.
=1.
∴g(x)在(﹣∞,x0)上单调递减,在(x0,+∞)上单调递增,
∴g(x)的最小值为g(x0)=![]() +x0
+x0![]() ﹣
﹣![]() ﹣x0+2=3﹣(
﹣x0+2=3﹣(![]() +x0),
+x0),
∵0<x0<ln2,∴1<![]() <2,∴
<2,∴![]() +x0<2+ln2<3,∴g(x0)=3﹣(
+x0<2+ln2<3,∴g(x0)=3﹣(![]() +x0)>0,
+x0)>0,
∴当![]() =1时,g(x)≥0在R上恒成立.
=1时,g(x)≥0在R上恒成立.
②当![]() =2时,g(x)=ex+(x﹣2)ex﹣2x+2,
=2时,g(x)=ex+(x﹣2)ex﹣2x+2,![]() =xex﹣2,g
=xex﹣2,g![]() (x)=(x+1)ex,
(x)=(x+1)ex,
由①可知![]() 在(﹣∞,﹣1)上单调递减,在(﹣1,+∞)上单调递增,
在(﹣∞,﹣1)上单调递减,在(﹣1,+∞)上单调递增,
![]() 的最小值为g
的最小值为g![]() (﹣1)=﹣
(﹣1)=﹣![]() ﹣2<0,且当x<0时,
﹣2<0,且当x<0时,![]() <0,g
<0,g![]() (ln2)=2ln2﹣2<0,g
(ln2)=2ln2﹣2<0,g![]() (1)=e﹣2>0,
(1)=e﹣2>0,
∴存在唯一一个实数x0∈(ln2,1),使得g![]() (x0)=0,即x0
(x0)=0,即x0![]() =2.
=2.
∴g(x)在(﹣∞,x0)上单调递减,在(x0,+∞)上单调递增,
∴g(x)的最小值为g(x0)=![]() +x0
+x0![]() ﹣
﹣![]() ﹣2x0+2=4﹣(
﹣2x0+2=4﹣(![]() +2x0),
+2x0),
∵ln2<x0<1,∴2<![]() <e,∴
<e,∴![]() +2x0>2+2ln2>4,∴g(x0)=3﹣(
+2x0>2+2ln2>4,∴g(x0)=3﹣(![]() +x0)<0,
+x0)<0,
∴当![]() =2时,g(x)≥0在R上不恒成立.
=2时,g(x)≥0在R上不恒成立.
综上,实数![]() 能取到的最大整数值为1.
能取到的最大整数值为1.


科目:高中数学 来源: 题型:
【题目】从某企业的某种产品中抽取![]() 件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
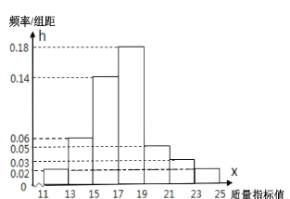
(Ⅰ)求这![]() 件产品质量指标值的样本平均数
件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表,记作
(同一组数据用该区间的中点值作代表,记作![]() ,
,![]() );
);
(Ⅱ)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)若使![]() 的产品的质量指标值高于企业制定的合格标准,则合格标准的质量指标值大约为多少?
的产品的质量指标值高于企业制定的合格标准,则合格标准的质量指标值大约为多少?
(ii)若该企业又生产了这种产品![]() 件,且每件产品相互独立,则这
件,且每件产品相互独立,则这![]() 件产品质量指标值不低于
件产品质量指标值不低于![]() 的件数最有可能是多少?
的件数最有可能是多少?
附:参考数据与公式:![]() ,
,![]() ;若
;若![]() ,则①
,则①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,且∠AOC=120°,PA⊥平面ABC,AB=4,PA=2![]() ,D是PC的中点,点M是⊙O上的动点(不与A,C重合).
,D是PC的中点,点M是⊙O上的动点(不与A,C重合).
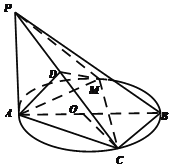
(1)证明:AD⊥PB;
(2)当三棱锥D﹣ACM体积最大时,求面MAD与面MCD所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:![]() ):男生成绩在175
):男生成绩在175![]() 以上(包括175
以上(包括175![]() )定义为“合格”,成绩在175
)定义为“合格”,成绩在175![]() 以下(不包括175
以下(不包括175![]() )定义为“不合格”.女生成绩在165
)定义为“不合格”.女生成绩在165![]() 以上(包括165
以上(包括165![]() )定义为“合格”,成绩在165
)定义为“合格”,成绩在165![]() 以下(不包括165
以下(不包括165![]() )定义为“不合格”.
)定义为“不合格”.
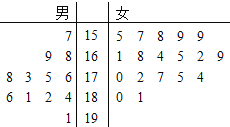
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用![]() 表示其中男生的人数,写出
表示其中男生的人数,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 且
且![]() ),且数列
),且数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() 的最小值;
的最小值;
(3)若![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 是递增数列?若存在,求出
是递增数列?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的前n项和为
的前n项和为![]() ,记
,记![]() ,
, ![]() ,…,
,…, ![]() 中奇数的个数为
中奇数的个数为![]() .
.
(Ⅰ)若![]() = n,请写出数列
= n,请写出数列![]() 的前5项;
的前5项;
(Ⅱ)求证:"![]() 为奇数,
为奇数, ![]() (i = 2,3,4,...)为偶数”是“数列
(i = 2,3,4,...)为偶数”是“数列![]() 是单调递增数列”的充分不必要条件;
是单调递增数列”的充分不必要条件;
(Ⅲ)若![]() ,i=1, 2, 3,…,求数列
,i=1, 2, 3,…,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com