
 中,
中,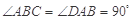 ,
,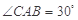 ,
,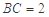 ,
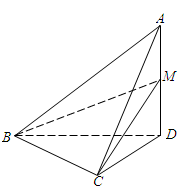
,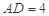 . 把
. 把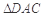 沿对角线
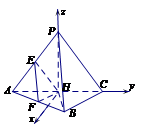
沿对角线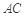 折起到
折起到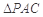 的位置,如图2所示,使得点
的位置,如图2所示,使得点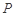 在平面
在平面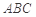 上的正投影
上的正投影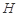 恰好落在线段
恰好落在线段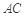 上,连接
上,连接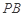 ,点
,点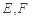 分别为线段
分别为线段 的中点.
的中点. 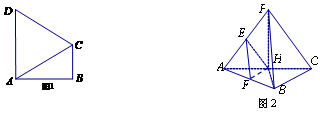
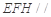 平面
平面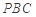 ;
;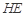 与平面
与平面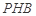 所成角的正弦值;
所成角的正弦值;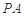 上是否存在一点
上是否存在一点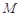 ,使得
,使得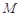 到点
到点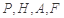 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.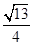 ;(3)存在,点E即为所求.
;(3)存在,点E即为所求.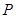 的正投影
的正投影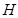 在
在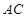 上得
上得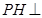 平面
平面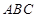 ,利用线面垂直的性质,得
,利用线面垂直的性质,得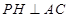 ,在原直角梯形中,利用已知的边和角,得到
,在原直角梯形中,利用已知的边和角,得到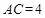 ,
,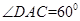 ,所以得到
,所以得到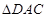 为等边三角形,从而知
为等边三角形,从而知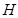 是
是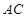 的中点,所以可得
的中点,所以可得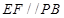 ,
,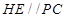 ,
,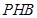 的法向量
的法向量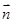 ,利用
,利用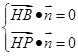 求出
求出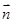 ,利用夹角公式求直线
,利用夹角公式求直线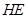 和法向量
和法向量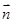 所在直线的夹角;第三问,由已知和前2问过程中得到的数据,可以看出
所在直线的夹角;第三问,由已知和前2问过程中得到的数据,可以看出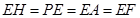 ,所以
,所以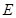 点即为所求.
点即为所求.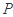 在平面
在平面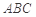 上的正投影
上的正投影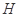 恰好落在线段
恰好落在线段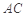 上,
上,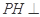 平面
平面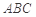 ,所以
,所以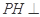
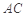 , 1分
, 1分 中,
中,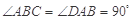 ,
,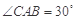 ,
,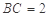 ,
,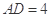 ,
,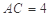 ,
,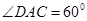 ,所以
,所以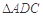 是等边三角形,
是等边三角形,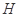 是
是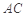 中点, 2分
中点, 2分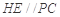 , 3分
, 3分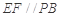 ,
,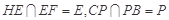 ,
,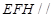 平面
平面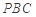 . 5分
. 5分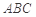 内过
内过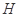 作
作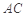 的垂线 如图建立空间直角坐标系,则
的垂线 如图建立空间直角坐标系,则 ,
,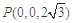 ,
,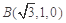 , 6分
, 6分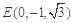 ,
,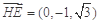 ,
,
 的法向量为
的法向量为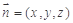 ,
,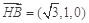 ,
,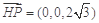 ,
, ,即
,即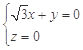 ,
,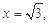 则
则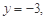 所以
所以 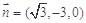 , 8分
, 8分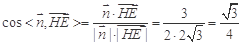 , 10分
, 10分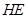 与平面
与平面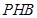 所成角的正弦值为
所成角的正弦值为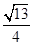 . 11分
. 11分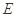 为
为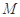 即可 12分
即可 12分 中,
中,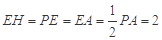 , 13分
, 13分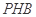 中,点
中,点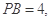
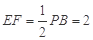 ,
, 到四个点
到四个点 的距离相等. 14分
的距离相等. 14分

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:不详 题型:解答题
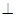 平面ADC;
平面ADC;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
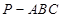 中,
中,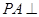 平面
平面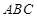 ,
,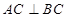 ,
,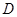 为侧棱
为侧棱 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.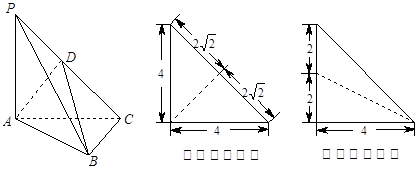
 平面
平面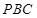 ;
;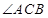 的平分线上确定一点
的平分线上确定一点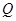 ,使得
,使得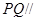 平面
平面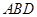 ,并求此时
,并求此时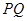 的长.
的长.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 平面CDE,AE=3.
平面CDE,AE=3.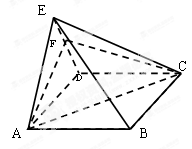
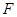 为
为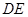 的中点,求证:
的中点,求证: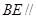 平面
平面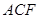 ;
;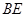 与平面
与平面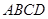 所成角的正弦值.
所成角的正弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
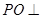 平面
平面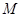 ,垂足为
,垂足为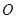 ,直线
,直线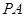 是平面
是平面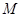 的一条斜线,斜足为
的一条斜线,斜足为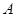 ,其中
,其中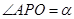 ,过点
,过点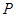 的动直线
的动直线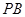 交平面
交平面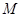 于点
于点 ,
,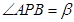 ,则下列说法正确的是___________.
,则下列说法正确的是___________.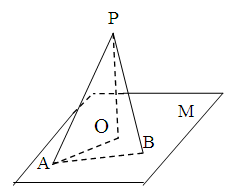
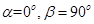 ,则动点B的轨迹是一个圆;
,则动点B的轨迹是一个圆;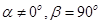 ,则动点B的轨迹是一条直线;
,则动点B的轨迹是一条直线;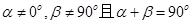 ,则动点B的轨迹是抛物线;
,则动点B的轨迹是抛物线;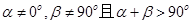 ,则动点B的轨迹是椭圆;
,则动点B的轨迹是椭圆;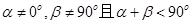 ,则动点B的轨迹是双曲线.
,则动点B的轨迹是双曲线.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
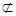 α,则n∥α;
α,则n∥α;| A.①② | B.②③ | C.③④ | D.②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com