
【题目】已知圆柱OO1底面半径为1,高为π,ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线Γ如图所示.将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1与曲线Γ相交于点P.

(1)求曲线Γ长度;
(2)当![]() 时,求点C1到平面APB的距离;
时,求点C1到平面APB的距离;
(3)是否存在θ,使得二面角D﹣AB﹣P的大小为![]() ?若存在,求出线段BP的长度;若不存在,请说明理由.
?若存在,求出线段BP的长度;若不存在,请说明理由.
【答案】(1)![]() π;(2)
π;(2)![]() ;(3)不存在,理由见解析
;(3)不存在,理由见解析
【解析】
(1)将圆柱一半展开后底面的半个圆周变成长方形的边BA,曲线Γ就是对角线BD,从而可求曲线Γ长度;
(2)当θ![]() 时,点B1恰好为AB的中点,所以P为B1C1中点,故点C1到平面APB的距离与点B1到平面APB的距离相等.
时,点B1恰好为AB的中点,所以P为B1C1中点,故点C1到平面APB的距离与点B1到平面APB的距离相等.
(3)由于二面角D﹣AB﹣B1为直二面角,故只要考查二面角P﹣AB﹣B1是否为![]() 即可.
即可.
解:(1)将圆柱一半展开后底面的半个圆周变成长方形的边BA,曲线Γ就是对角线BD.
由于AB=πr=π,AD=π,所以这实际上是一个正方形.
所以曲线Γ的长度为BD![]() π.
π.
(2)当θ![]() 时,点B1恰好为AB的中点,所以P为B1C1中点,
时,点B1恰好为AB的中点,所以P为B1C1中点,
故点C1到平面APB的距离与点B1到平面APB的距离相等.
连接AP、BP,OP.
由AB⊥B1P且AB⊥A1B1知:AB⊥平面A1B1P,从而平面A1B1P⊥平面APB.
作B1H⊥OP于H,则B1H⊥平面APB,所以B1H即为点B1到平面APB的距离.
在Rt△OB1P中,![]()
由(1)可知,圆柱的一半展开后得到一个正方形,所以![]()
所以 .
.
于是: .
.
所以,点C1到平面APB的距离为![]() .
.
(3)由于二面角D﹣AB﹣B1为直二面角,故只要考查二面角P﹣AB﹣B1是否为![]() 即可.
即可.
过B1作B1Q⊥AB于Q,连接PQ.
由于B1Q⊥AB,B1P⊥AB,所以AB⊥平面B1PQ,所以AB⊥PQ.
于是∠PQB1即为二面角P﹣AB﹣B1的平面角.
在Rt△PB1Q中,![]() .
.
由(2)有![]()
若![]() ,则需B1P=B1Q,即sinθ=θ.
,则需B1P=B1Q,即sinθ=θ.
令f(x)=sinx﹣x(0<x<π),则f′(x)=cosx﹣1<0,
故f(x)在(0,π)单调递减.
所以f(x)<f(0)=0,即sinx<x在(0,π)上恒成立.
故不存在θ∈(0,π),使sinθ=θ.
也就是说,不存在θ∈(0,π),使二面角D﹣AB﹣P为![]() .
.




 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到:任画…条线段,然后把它分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了由4条小线段构成的折线,称为“一次构造”;用同样的方法把每一条小线段重复上述步骤,得到由16条更小的线段构成的折线,称为“二次构造”;…;如此进行“n次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度大于初始线段的100倍,则至少需要构造的次数是( )(取![]() ,
,![]() )
)

A.16B.17C.24D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为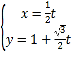 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 且
且![]() ).
).
(I)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是曲线
是曲线![]() 上的一点,
上的一点, ![]() ,
,![]() ,若
,若![]() 的最大值为2,求
的最大值为2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() ,在
,在![]() 轴正半轴上有一点
轴正半轴上有一点![]() ,过点
,过点![]() 作直线
作直线![]() ,
,![]() 分别交抛物线于点
分别交抛物线于点![]() ,过点
,过点![]() 作
作![]() 垂直于
垂直于![]() 轴分别交
轴分别交![]() 于点
于点![]() .当
.当![]() ,直线
,直线![]() 的斜率为1时,
的斜率为1时,![]() .
.
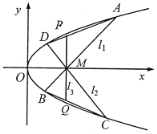
(1)求抛物线的方程;
(2)判断![]() 是否为定值,若是,求出此定值;若不是,请说明理由.
是否为定值,若是,求出此定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为![]() 曲线C的参数方程为
曲线C的参数方程为 .
.
(1)求曲线C的右顶点到直线l的距离;
(2)若点P的坐标为(1,1),设直线l与曲线C交于A,B两点,求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 与曲线
与曲线![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,已知![]() 与
与![]() ,
,![]() 的公共点分别为
的公共点分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的零点构成一个公差为
的零点构成一个公差为![]() 的等差数列,把函数
的等差数列,把函数![]() 的图象沿
的图象沿![]() 轴向右平移
轴向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.关于函数
的图象.关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 在![]() 上是增函数B. 其图象关于直线
上是增函数B. 其图象关于直线![]() 对称
对称
C. 函数![]() 是偶函数D. 在区间
是偶函数D. 在区间![]() 上的值域为
上的值域为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 越大,说明“
越大,说明“![]() 与
与![]() 有关系”的可信度越大;
有关系”的可信度越大;
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和
和![]() ;
;
③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
④若变量![]() 和
和![]() 满足关系
满足关系![]() ,且变量
,且变量![]() 与
与![]() 正相关,则
正相关,则![]() 与
与![]() 也正相关.
也正相关.
正确的个数是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com