练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，棱长为a的正方体，N是棱的中点；

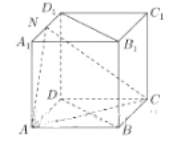
    （1）求直线AN与平面所成角的大小；

    （2）求到平面ANC的距离.

    【答案】（1）；（2）a；

    【解析】

    （1）以为原点，建立空间直角坐标系，求出平面的一个法向量，利用向量的夹角公式，得到与法向量的夹角，从而得到答案；（2）求出平面的一个法向量，到平面的距离等于在此法向量方向上投影的绝对值，从而得到答案.

    （1）以为坐标原点，为轴，为轴，为轴，

    建立空间直角坐标系，如图所示，

    则，，，，

    因为平面，平面，

    所以，

    因为正方形，所以

    平面，，

    所以平面，

    故为平面的一个法向量，，

    ，

    设直线与平面所成的角为，

    则，

    所以直线与平面所成的角为.

    （2）设平面的一个法向量，

    则，所以，

    取，

    因为，

    所以到平面的距离.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】有下列四个命题：（1）一定存在直线，使函数的图像与函数的图像关于直线对称；（2）不等式：的解集为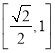；（3）已知数列的前项和为，，则数列一定是等比数列；（4）过抛物线上的任意一点的切线方程一定可以表示为.则正确命题的序号为_________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    (1)若,求函数的单调区间;

    (2)若对恒成立,求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司欲对员工饮食习惯进行一次调查，从某科室的100人中的饮食结构调查结果统计如下表.

    主食蔬菜

    主食肉类

    总计

    不超过45岁

    15

    40

    45岁以上

    20

    总计

    （1）完成列联表，并判断能否有99%的把握认为员工的饮食习惯与年龄有关？

    （2）在45岁以上员工中按照饮食习惯进行分层抽样抽出一个容量为6的样本，从这6个人中随机抽取3个人，求这3个人都主食蔬菜的概率.

    附：

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】每年9月第三周是国家网络安全宣传周.某学校为调查本校学生对网络安全知识的了解情况，组织了《网络信息辨析测试》活动，并随机抽取50人的测试成绩绘制了频率分布直方图如图所示:

    （1）某学生的测试成绩是75分，你觉得该同学的测试成绩低不低?说明理由；

    （2）将成绩在内定义为“合格”；成绩在内定义为“不合格”.①请将下面的列联表补充完整； ②是否有90%的把认为网络安全知识的掌握情况与性别有关?说明你的理由；

    合格

    不合格

    合计

    男生

    26

    女生

    6

    合计

    （3）在（2）的前提下，对50人按是否合格，利用分层抽样的方法抽取5人，再从5人中随机抽取2人，求恰好2人都合格的概率.附:

    0.100

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一款手游，页面上有一系列的伪装，其中隐藏了4个宝藏．如果你在规定的时间内找到了这4个宝藏，将会弹出下一个页面，这个页面仍隐藏了2个宝藏，若能在规定的时间内找到这2个宝藏，那么闯关成功，否则闯关失败，结束游戏；如果你在规定的时间内找到了3个宝藏，仍会弹出下一个页面，但这个页面隐藏了4个宝藏，若能在规定的时间内找到这4个宝藏，那么闯关成功，否则闯关失败，结束游戏；其它情况下，不会弹出下一个页面，闯关失败，并结束游戏．

    假定你找到任何一个宝藏的概率为，且能否找到其它宝藏相互独立．．

    （1）求闯关成功的概率；

    （2）假定你付1个Q币游戏才能开始，能进入下一个页面就能获得2个Q币的奖励，闯关成功还能获得另外4个Q币的奖励，闯关失败没有额外的奖励．求一局游戏结束，收益的Q币个数X的数学期望（收益=收入-支出）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程是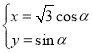（是参数）.以原点为极点，以轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程是.

    （1）求曲线的普通方程与曲线的直角坐标方程；

    （2）设为曲线上的动点，过点且与垂直的直线交于点，求的最小值，并求此时点的直角坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设命题p：实数x满足x2﹣4ax+3a2＜0（a＞0），命题q：实数x满足x2﹣5x+6＜0．

    （1）若a＝1，且p∧q为真命题，求实数x的取值范围；

    （2）若p是q的必要不充分条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，左、右焦点分别是，椭圆上短轴的一个端点与两个焦点构成的三角形的面积为；

    （1）求椭圆的方程；

    （2）过作垂直于轴的直线交椭圆于两点（点在第二象限），是椭圆上位于直线两侧的动点，若，求证：直线的斜率为定值.

    查看答案和解析>>

    同步练习册答案