
【题目】(12分)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
【答案】(Ⅰ)an=1+(n﹣1)×(﹣2)=3﹣2n(Ⅱ)k=7
【解析】试题(I)设出等差数列的公差为d,然后根据首项为1和第3项等于﹣3,利用等差数列的通项公式即可得到关于d的方程,求出方程的解即可得到公差d的值,根据首项和公差写出数列的通项公式即可;
(II)根据等差数列的通项公式,由首项和公差表示出等差数列的前k项和的公式,当其等于﹣35得到关于k的方程,求出方程的解即可得到k的值,根据k为正整数得到满足题意的k的值.
解:(I)设等差数列{an}的公差为d,则an=a1+(n﹣1)d
由a1=1,a3=﹣3,可得1+2d=﹣3,解得d=﹣2,
从而,an=1+(n﹣1)×(﹣2)=3﹣2n;
(II)由(I)可知an=3﹣2n,
所以Sn=![]() =2n﹣n2,
=2n﹣n2,
进而由Sk=﹣35,可得2k﹣k2=﹣35,
即k2﹣2k﹣35=0,解得k=7或k=﹣5,
又k∈N+,故k=7为所求.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知递减等差数列{an}满足:a1=2,a2a3=40. (Ⅰ)求数列{an}的通项公式及前n项和Sn;
(Ⅱ)若递减等比数列{bn}满足:b2=a2 , b4=a4 , 求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某学校组织的一次篮球总投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分,如果前两次得分之和超过3分即停止投篮,否则投第3次.某同学在A处的命中率q1为0.25,在B处的命中率为q2 . 该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮的训练结束后所得的总分,其分布列为
ξ | 0 | 2 | 3 | 4 | 5 |
P | 0.03 | P1 | P2 | P3 | P4 |
(1)求q2的值;
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=92n﹣1 , n∈N* . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=nan , 数列{bn}的前n项和为Sn , 若不等式Sn>kan﹣1对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA= ![]() .
. 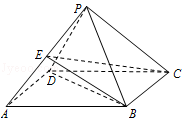
(Ⅰ)求证:BD⊥PC;
(Ⅱ)若E是PA的中点,求三棱锥P﹣BCE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空中有一气球,在它的正西方A点测得它的仰角为45°,同时在它南偏东60°的B点,测得它的仰角为30°,已知A、B两点间的距离为107米,这两个观测点均离地1米,则测量时气球离地的距离是_____米.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)是定义在R上的偶函数,f(x+1)为奇函数,f(0)=0,当x∈(0,1]时,f(x)=log2x,则在区间(8,9)内满足方f(x)程f(x)+2=f( ![]() )的实数x为( )
)的实数x为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com