
| A. | 5 | B. | 1 | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
分析 设M(x1,a),N(x2,a),则4x1+4=3x2+lnx2,表示出x1,求出|MN|,利用导数求出|MN|的最小值.
解答 解:设M(x1,a),N(x2,a),
则4x1+4=3x2+lnx2,
∴x1=$\frac{1}{4}$(3x2+lnx2-4),
∴|MN|=x2-x1=$\frac{1}{4}$(x2-lnx2)+1,
令y=$\frac{1}{4}$(x-lnx)+1,
则y′=$\frac{1}{4}$(1-$\frac{1}{x}$),
函数在(0,1)上单调递减,在(1,+∞)上单调递增,
∴x=1时,函数的最小值为$\frac{5}{4}$.
故选:C.
点评 本题考查两点间距离的最小值的求法,是中档题,考查学生分析解决问题的能力,正确求导确定函数的单调性是关键.解题时要认真审题,注意导数性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
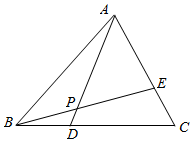 在△ABC中,点D和E分别在边BC和AC上,且BC=3BD,CA=3CE,AD与BE交于点P,若$\overrightarrow{AP}$=m$\overrightarrow{AD}$,$\overrightarrow{BP}$=n$\overrightarrow{BE}$(m,n∈R),则m+n=$\frac{9}{7}$.
在△ABC中,点D和E分别在边BC和AC上,且BC=3BD,CA=3CE,AD与BE交于点P,若$\overrightarrow{AP}$=m$\overrightarrow{AD}$,$\overrightarrow{BP}$=n$\overrightarrow{BE}$(m,n∈R),则m+n=$\frac{9}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-1] | B. | [-2,1] | C. | [-1,2] | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{8}$,0) | B. | (-$\frac{π}{4}$,0) | C. | ($\frac{π}{8}$,0) | D. | ($\frac{π}{4}$,0) |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:解答题
已知椭圆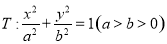 的离心率为
的离心率为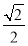 ,过左焦点
,过左焦点 的直线与椭圆交于
的直线与椭圆交于 两点,若线段
两点,若线段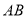 的中点为
的中点为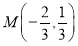 .
.
(1)求椭圆的方程;
(2)过右焦点的直线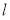 与圆
与圆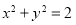 相交于
相交于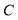 、
、 ,与椭圆
,与椭圆 相交于
相交于 、
、 ,且
,且 ,求
,求 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com