
| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于直线x=$\frac{π}{12}$对称 | ||
| C. | 关于点($\frac{5}{12}$π,0)对称 | D. | 关于直线x=$\frac{5}{12}$π对称 |
分析 由已知其周期公式可求ω=2,再由f(x)=sin(2x+φ)向左移$\frac{π}{6}$个单位得f(x)=sin(2x+$\frac{π}{3}$+φ)为奇函数,则有$\frac{π}{3}$+φ=kπ(k∈Z),|φ|<$\frac{π}{2}$,可求 φ 代入选项检验.
解答 解:由已知T=$\frac{2π}{ω}$,则ω=2,
f(x)=sin(2x+φ)向左移$\frac{π}{6}$个单位得f(x)=sin[2(x+$\frac{π}{6}$)+φ]=sin(2x+$\frac{π}{3}$+φ)为奇函数,
则有:$\frac{π}{3}$+φ=kπ(k∈Z),
∵|φ|<$\frac{π}{2}$,
∴φ=-$\frac{π}{3}$,可得:f(x)=sin(2x-$\frac{π}{3}$).
代入选项检验,当x=$\frac{5π}{12}$时,f($\frac{5π}{12}$)=sin$\frac{π}{2}$=1为函数的最大值,
根据三角函数的性质可知对称轴处将取得函数的最值,D正确.
故选:D.
点评 本题主要考查了正弦函数的图象和性质,考查了函数y=Asin(ωx+φ)的图象变换规律,由三角函数的部分图象的性质求解函数的解析式的关键是要熟练应用函数的性质,还要注意排除法在解题中的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
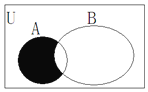
| A. | (-1,1) | B. | [-1,1] | C. | [1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
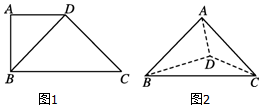 如图1所示,在四边形ABCD中,AD∥BC,AD=AB=1,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥ABCD(如图2)
如图1所示,在四边形ABCD中,AD∥BC,AD=AB=1,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥ABCD(如图2)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (2,3) | C. | [0,2) | D. | (0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com