
【题目】已知函数![]() .
.
(1)讨论![]() 的单调区间;
的单调区间;
(2)当![]() 时,证明:
时,证明: ![]() .
.
科目:高中数学 来源: 题型:
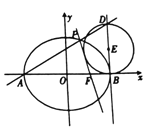
【题目】如图,设椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为右焦点,直线
为右焦点,直线![]() 与
与![]() 的交点到
的交点到![]() 轴的距离为
轴的距离为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
, ![]() 为
为![]() 上异于点
上异于点![]() 的一点,以
的一点,以![]() 为直径作圆
为直径作圆![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,证明:直线
,证明:直线![]() 与圆
与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于A、B、C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中:
(1)恰有2人申请A片区房源的概率;
(2)申请的房源所在片区的个数的ξ分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①幂函数f(x)= ![]() 的单调递减区间是(﹣∞,0)∪(0,+∞);
的单调递减区间是(﹣∞,0)∪(0,+∞);
②若函数f(x+2016)=x2﹣2x﹣1(x∈R),则函数f(x)的最小值为﹣2;
③若函数f(x)=loga|x|(a>0,a≠1)在(0,+∞)上单调递增,则f(﹣2)<f(a+1);
④若f(x)= ![]() 是(﹣∞,+∞)上的减函数,则a的取值范围是(
是(﹣∞,+∞)上的减函数,则a的取值范围是( ![]() ,
, ![]() );
);
⑤既是奇函数,又是偶函数的函数一定是f(x)=0(x∈R).
其中正确命题的序号有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于函数f(x),若在定义域内存在实数x,满足f(﹣x)=﹣f(x),则称f(x)为“局部奇函数”.
(1)已知二次函数f(x)=ax2+2x﹣4a(a∈R),试判断f(x)是否为定义域R上的“局部奇函数”?若是,求出满足f(﹣x)=﹣f(x)的x的值;若不是,请说明理由;
(2)若f(x)=2x+m是定义在区间[﹣1,1]上的“局部奇函数”,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的焦点是F1、F2 , 且|F1F2|=2,离心率为
=1(a>b>0)的焦点是F1、F2 , 且|F1F2|=2,离心率为 ![]() . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)若过椭圆右焦点F2的直线l交椭圆于A,B两点,求|AF2||F2B|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax,(a∈R)
(1)若函数f(x)在点区间[e,+∞]处上为增函数,求a的取值范围;
(2)若函数f(x)的图象在点x=e(e为自然对数的底数)处的切线斜率为3,且k∈Z时,不等式 k(x﹣1)<f(x)在x∈(1,+∞)上恒成立,求k的最大值;
(3)n>m≥4时,证明:(mnn)m>(nmm)n .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足 ![]() <0,其中a>0,命题q:实数x满足
<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com