
【题目】己知函数f(x)=(x+l)lnx﹣ax+a (a为正实数,且为常数)
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范围.
【答案】
(1)解:f(x)=(x+l)lnx﹣ax+a,f′(x)=lnx+ ![]() +1﹣a,
+1﹣a,
若f(x)在(0,+∞)上单调递增,
则a≤lnx+ ![]() +1在(0,+∞)恒成立,(a>0),
+1在(0,+∞)恒成立,(a>0),
令g(x)=lnx+ ![]() +1,(x>0),
+1,(x>0),
g′(x)= ![]() ,
,
令g′(x)>0,解得:x>1,令g′(x)<0,解得:0<x<1,
故g(x)在(0,1)递减,在(1,+∞)递增,
故g(x)min=g(1)=2,
故0<a≤2;
(2)解:若不等式(x﹣1)f(x)≥0恒成立,
即(x﹣1)[(x+1)lnx﹣a]≥0恒成立,
①x≥1时,只需a≤(x+1)lnx恒成立,
令m(x)=(x+1)lnx,(x≥1),
则m′(x)=lnx+ ![]() +1,
+1,
由(1)得:m′(x)≥2,
故m(x)在[1,+∞)递增,m(x)≥m(1)=0,
故a≤0,而a为正实数,故a≤0不合题意;
②0<x<1时,只需a≥(x+1)lnx,
令n(x)=(x+1)lnx,(0<x<1),
则n′(x)=lnx+ ![]() +1,由(1)n′(x)在(0,1)递减,
+1,由(1)n′(x)在(0,1)递减,
故n′(x)>n(1)=2,
故n(x)在(0,1)递增,故n(x)<n(1)=0,
故a≥0,而a为正实数,故a>0.
【解析】(1)求出函数f(x)的导数,问题转化为a≤lnx+ ![]() +1在(0,+∞)恒成立,(a>0),令g(x)=lnx+
+1在(0,+∞)恒成立,(a>0),令g(x)=lnx+ ![]() +1,(x>0),根据函数的单调性求出a的范围即可;(2)问题转化为(x﹣1)[(x+1)lnx﹣a]≥0恒成立,通过讨论x的范围,结合函数的单调性求出a的范围即可.
+1,(x>0),根据函数的单调性求出a的范围即可;(2)问题转化为(x﹣1)[(x+1)lnx﹣a]≥0恒成立,通过讨论x的范围,结合函数的单调性求出a的范围即可.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则
,则
(![]() )函数
)函数![]() 定义域为__________.
定义域为__________.
(![]() )函数
)函数![]() 导函数为
导函数为![]() __________.
__________.
(![]() )对函数
)对函数![]() 单调研究如下
单调研究如下
| |||||
|
|
| |||
|
____
(![]() )设函数
)设函数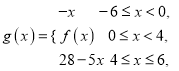 则
则
函数![]() 的最大值为__________.
的最大值为__________.
(5)函数![]() 极值点共__________个,(6)其中极小值点有__________个.
极值点共__________个,(6)其中极小值点有__________个.
(7)若关于![]() 的方程
的方程![]() 恰有三个不相同的实数解,则
恰有三个不相同的实数解,则![]() 的取值范围为__________.
的取值范围为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,
, ![]() 为圆
为圆![]() 上一点,线段
上一点,线段![]() 上一点
上一点![]() 满足
满足![]() ,直线
,直线![]() 上一点
上一点![]() ,满足
,满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 为坐标原点,
为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹
相切,并与轨迹![]() 交于不同的两点
交于不同的两点![]() .当
.当![]() 且满足
且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
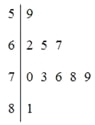
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图4所示,求该样本的方差;
(3)在(2)的条件下,从这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线![]() 和
和![]() 是异面直线,
是异面直线,![]() 在平面
在平面![]() 内,
内,![]() 在平面
在平面![]() 内,
内,![]() 是平面
是平面![]() 与平面
与平面![]() 的交线,则下列结论正确的是( )
的交线,则下列结论正确的是( )
A. ![]() 至少与
至少与![]() ,
,![]() 中的一条相交 B.
中的一条相交 B. ![]() 与
与![]() ,
,![]() 都不相交
都不相交
C. ![]() 与
与![]() ,
,![]() 都相交 D.
都相交 D. ![]() 至多与
至多与![]() ,
,![]() 中的一条相交
中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】在三棱锥![]() 中,因为
中,因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,则该几何体的外接球即为以
,则该几何体的外接球即为以![]() 为棱长的长方体的外接球,则
为棱长的长方体的外接球,则![]() ,其体积为
,其体积为![]() ;故选D.
;故选D.
点睛:在处理几何体的外接球问题,往往将所给几何体与正方体或长方体进行联系,常用补体法补成正方体或长方体进行处理,本题中由数量关系可证得![]()
![]() 从而几何体的外接球即为以
从而几何体的外接球即为以![]() 为棱长的长方体的外接球,也是处理本题的技巧所在.
为棱长的长方体的外接球,也是处理本题的技巧所在.
【题型】单选题
【结束】
21
【题目】已知函数![]() ,则
,则![]() 的大致图象为( )
的大致图象为( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com