
(08年金华一中) 如图,已知正三棱柱![]() ,
, ![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ∥平面
∥平面![]() 。记
。记![]() 。
。
(1)求![]() 的值;
的值;
(2)若∠![]() ,求二面角
,求二面角![]() 的大小;
的大小;

解析:(1)连结![]() 交
交![]() 于O,则O是
于O,则O是![]() 的中点,连结DO。
的中点,连结DO。
∵![]() ∥平面
∥平面![]() ,∴
,∴![]() ∥DO
∥DO
∴D为AC中点,∴![]()
(2)设正三棱柱底面边长为2,则DC = 1。
∵∠![]() = 60°,∴
= 60°,∴![]() =
= ![]() 。
。
作DE⊥BC于E。∵平面![]() ⊥平面ABC,
⊥平面ABC,
∴DE⊥平面![]()
![]() ,作EF⊥
,作EF⊥![]() 于F,连结DF,则 DF⊥
于F,连结DF,则 DF⊥![]()
∴∠DFE是二面角D-![]() -C的平面角
-C的平面角
在Rt△DEC中,DE=![]() ,在Rt△BFE中,EF = BE?sin∠
,在Rt△BFE中,EF = BE?sin∠![]()
∴在Rt△DEF中,tan∠DFE = ![]()
∴二面角D-![]() -C的大小为arctan
-C的大小为arctan![]()

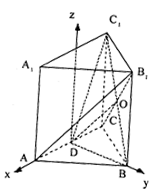
解法二:以AC的中D为原点建立坐标系,如图,
设| AD | = 1,∵∠![]() =60°∴|
=60°∴|![]() | =
| =![]() 。
。
则A(1,0,0),B(0,![]() ,0),C(-1,0,0),
,0),C(-1,0,0),
![]() (1,0
(1,0![]() ),
),![]() ,
,![]()
(2)![]() =(-1,0,
=(-1,0,![]() ),
),![]()
设平面B![]() D的法向量为
D的法向量为![]() ,则
,则![]() , 即
, 即
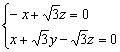 则有
则有![]() = 0令z = 1,则
= 0令z = 1,则![]() = (
= (![]() ,0,1)
,0,1)
设平面BC![]()
![]() 的法向量为
的法向量为![]() ,
,![]() =(0,0,
=(0,0,![]() ),
),![]()
 即
即![]() ∴z′= 0
∴z′= 0
令y = -1,解得![]() = (
= (![]() ,-1,0),
,-1,0),![]() ,
,
二面角D―B![]() ―C的大小为arc cos
―C的大小为arc cos![]()


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:
(08年金华一中理) (14分) 9粒种子分种在甲、乙、丙3个坑内,每坑3粒,每粒种子发芽的概率为0.5,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没有发芽,则这个坑需要补种。
(1)求甲坑不需要补种的概率;
(2)求3个坑中恰有1个坑不需要补种的概率;
(3)求有坑需要补种的概率。查看答案和解析>>
科目:高中数学 来源: 题型:
(08年金华一中理) (15分) 动圆![]() 过定点
过定点![]() 且与直线
且与直线![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,过
,过![]() 作曲线
作曲线![]() 两条互相垂直的弦
两条互相垂直的弦![]() ,设
,设![]() 的中点分别为
的中点分别为![]() 、
、![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)求证:直线![]() 必过定点;
必过定点;
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年金华一中理) (15分) 动圆![]() 过定点
过定点![]() 且与直线
且与直线![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,过
,过![]() 作曲线
作曲线![]() 两条互相垂直的弦
两条互相垂直的弦![]() ,设
,设![]() 的中点分别为
的中点分别为![]() 、
、![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)求证:直线![]() 必过定点;
必过定点;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com