
【题目】设定义域为R的函数f(x)= ![]() ,则关于x的方程f2(x)+bf(x)+c=0有5个不同的实数解xi(i=1,2,3,4,5),则f(x1+x2+x3+x4+x5+2)=( )
,则关于x的方程f2(x)+bf(x)+c=0有5个不同的实数解xi(i=1,2,3,4,5),则f(x1+x2+x3+x4+x5+2)=( )
A.![]()
B.![]()
C.2
D.1
 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}.满足:an+1>an(n∈N*),a1=1,该数列的前三项分别加上1,1,3后成等比数列,an+2log2bn=﹣1.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
. 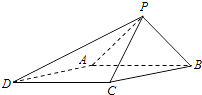
(1)求证:AB⊥PC;
(2)求二面角B一PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-1+![]() (a∈R,e为自然对数的底数).
(a∈R,e为自然对数的底数).
(1)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求a的值;
(2)当a=1时,若直线l:y=kx-1与曲线y=f(x)相切,求l的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)上点T(3,t)到焦点F的距离为4. 
(1)求t,p的值;
(2)设A,B是抛物线上分别位于x轴两侧的两个动点,且 ![]() (其中O为坐标原点).求证:直线AB过定点,并求出该定点的坐标.
(其中O为坐标原点).求证:直线AB过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1C, C1B1,C1D1的中点,点H在四边形A1ADD1的边及其内部运动,则H满足条件________时,有BH∥平面MNP.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某园林基地培育了一种新观赏植物,经过一年的生长发育,技术人员从中抽取了部分植株的高度(单位:厘米)作为样本(样本容量为![]() )进行统计,按照
)进行统计,按照![]()
![]() 的分组作出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了高度在
的分组作出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了高度在![]() 的数据).
的数据).
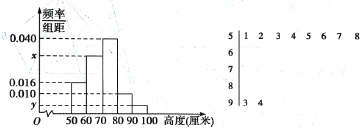
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从高度在![]() 厘米以上(含
厘米以上(含![]() 厘米)的植株中随机抽取
厘米)的植株中随机抽取![]() 株,求所取的
株,求所取的![]() 株中至少有一株高度在
株中至少有一株高度在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() +
+![]() =1(a>b>0)的短轴两端点为B1(0,﹣1)、B2(0,1),离心率e=
=1(a>b>0)的短轴两端点为B1(0,﹣1)、B2(0,1),离心率e=![]() ,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,
,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,

(1)求椭圆![]() 的方程和
的方程和![]() 的值;
的值;
(2)若点![]() 坐标为(1,0),过
坐标为(1,0),过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试求
两点,试求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com