
【题目】某班A、B两名学生六次数学测验成绩(百分制)如图所示:
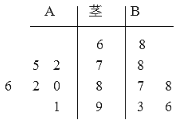
①A同学成绩的中位数大于B同学成绩的中位数;
②A同学的平均分比B同学高;
③A同学的平均分比B同学低;
④A同学成绩方差小于B同学的方差,
以上说法中正确的是( )
A.③④B.①②④C.②④D.①③④
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图(每个受访者都只能在问卷的5个活动中选择一个),以下结论错误的是( )

A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中,选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中,选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中,选择“公益广告”的人数比选择“学校要求”的少8个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点F到右准线的距离为3.
,右焦点F到右准线的距离为3.
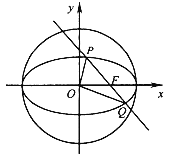
(1)求椭圆C的标准方程;
(2)设过F的直线l与椭圆C相交于P,Q两点.已知l被圆O:x2+y2=a2截得的弦长为![]() ,求△OPQ的面积.
,求△OPQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程,并说明它是何种曲线;
的直角坐标方程,并说明它是何种曲线;
(2)设点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,![]() 为正三角形,且侧面PAB⊥底面ABCD,
为正三角形,且侧面PAB⊥底面ABCD, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上.
上.
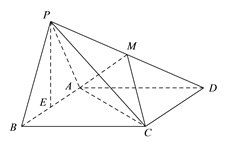
(I)当![]() 是线段
是线段![]() 的中点时,求证:PB // 平面ACM;
的中点时,求证:PB // 平面ACM;
(II)求证: ![]() ;
;
(III)是否存在点![]() ,使二面角
,使二面角![]() 的大小为60°,若存在,求出
的大小为60°,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆A:(x+2)2+y2=32,过B(2,0)且与圆A相切的动圆圆心为P.
(1)求点P的轨迹E的方程;
(2)设过点A的直线l1交曲线E于Q、S两点,过点B的直线l2交曲线E于R、T两点,且l1⊥l2,垂足为W(Q、S、R、T为不同的四个点),求四边形QRST的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,
,![]() 为
为![]() 上任意一点,
上任意一点,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过
,过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,证明:直线
两点,证明:直线![]() 的斜率与直线
的斜率与直线![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中左焦点
,其中左焦点![]() (-2,0).
(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com