
分析 (1)求出函数F(x)的导数,分离参数,问题转化为m≥ex-2x在[0,2]恒成立,令h(x)=ex-2x,x∈[0,2],根据函数的单调性求出m的范围即可;
(2)问题转化为证G(x)max≤H(x)min,根据函数的单调性分别求出G(x)的最大值和H(x)的最小值,从而证出结论.
解答 解:(1)∵F(x)=x2+mx+1-ex,
∴F′(x)=2x+m-ex,
∵x∈[0,2]时,F(x)是增函数,
∴F′(x)≥0即2x+m-ex≥0在[0,2]上恒成立,
即m≥ex-2x在[0,2]恒成立,
令h(x)=ex-2x,x∈[0,2],
则h′(x)=ex-2,令h′(x)=0,解得:x=ln2,
∴h(x)在[0,ln2]递减,在[ln2,2]递增,
∵h(0)=1,h(2)=e2-4>1,
∴h(x)max=h(2)=e2-4;
(2)G(x)=$\frac{{x}^{2}+mx+1}{{e}^{x}}$,
则G′(x)=-$\frac{(x-1)[x-(1-m)]}{{e}^{x}}$,
对任意x1,x2∈[1,1-m],G(x1)<H(x2)恒成立,
即证G(x)max≤H(x)min,
∵x∈[1,1-m],
∴G(x)在[1,1-m]递增,
G(x)max=G(1-m)=$\frac{2-m}{{e}^{1-m}}$,
∵H(x)在[1,1-m]递减,
H(x)min=H(1-m)=-$\frac{1}{4}$(1-m)+$\frac{5}{4}$,
要证G(x)max≤H(x)min,
即证$\frac{2-m}{{e}^{1-m}}$≤-$\frac{1}{4}$(1-m)+$\frac{5}{4}$,
即证4(2-m)≤e1-m[5-(1-m)],
令1-m=t,则t∈(1,2),
设r(x)=ex(5-x)-4(x+1),x∈[1,2],
即r(x)=5ex-xex-4x-4,
r′(x)=(4-x)ex-4≥2ex-4>0,
∴r(x)在[1,2]递增,
∵r(1)=4e-8>0,
∴ex(5-x)≥4(x+1),
从而有-$\frac{1}{4}$(1-m)+$\frac{5}{4}$≥$\frac{2-m}{{e}^{1-m}}$,
即当x∈[1,1-m],G(x1)<H(x2)恒成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<3} | B. | {-1,0,1} | C. | {x|-1<x<2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
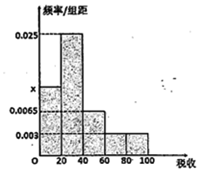 我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]
我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com