分析:(1)根据导数运算公式,得f'(x)=
,然后根据实数a的正负进行讨论,即可得到当a≤0时和当a>0时两种情况下函数f(x)的单调区间;
(2)当a=0时h(x)在(0,1)上有且只有一个极值点,即h'(x)=0在(0,1)上有且只有一个根且不为重根.因此求出h'(x)的表达式,再分b=0、b>0和b<0三种情况加以讨论,即可算出实数b的取值范围;
(3)首先根据(1)的结论,讨论可得只有0<a<
时直线l与y=F(x)的图象有两个切点.设切点的横坐标分别为s、t且s<t,可得l与y=F(x)的图象有两个切点分别为直线l与曲线
y1=--lnx在x∈(s,t)的切点和曲线
y2=+lnx在x∈(t,+∞)的切点.由此结合直线的斜率公式和导数的几何意义列出关于a、x
1、y
1、x
2、y
2的关系式,化简整理可得
=ln,再令
=k(0<k<1),转化为(k
2+1)lnk=2k
2-2.令G(k)=(k
2+1)lnk-2k
2+2,(0<k<1),由根的存在性定理证出:存在k
0∈(0,1),使得G(k
0)=0.由此即可得到原命题成立.
解答:解:(1)因为f'(x)=-
+
=
,
①若a≤0,则f'(x)>0,f(x)在(0,+∞)上为增函数,…(2分)
②若a>0,令f'(x)=0,得x=a,
当0<x<a时,f'(x)<0;当x>a时,f'(x)>0.
所以(0,a)为单调减区间,(a,+∞)为单调增区间.
综上可得,当a≤0时,函数f(x)在(0,+∞)上为增函数,
当a>0时,函数f(x)的单调减区间为(0,a),单调增区间为(a,+∞). …(4分)
(2)a=0时,h(x)=f(x)+g(x)=
bx2-2x+2+lnx,
∴h'(x)=bx-2+
=
,…(5分)
h(x)在(0,1)上有且只有一个极值点,即h'(x)=0在(0,1)上有且只有一个根且不为重根,
由h'(x)=0得bx
2-2x+1=0,…(6分)
( i)b=0,x=
,满足题意;…(7分)
( ii)b>0时,b•1
2-2•1+1<0,即0<b<1;…(8分)
( iii)b<0时,b•1
2-2•1+1<0,得b<1,故b<0;
综上所述,得:h(x)在(0,1)上有且只有一个极值点时,b<1. …(9分)
(3)证明:由(1)可知:
( i)若a≤0,则f'(x)≥0,f(x)在(0,+∞)上为单调增函数,
所以直线l与y=F(x)的图象不可能有两个切点,不合题意.…(10分)
(ⅱ)若a>0,f(x)在x=a处取得极值f(a)=1+lna.
若1+lna≥0,a≥
时,由图象知不可能有两个切点.…(11分)
故0<a<
,设f(x)图象与x轴的两个切点的横坐标为s,t(不妨设s<t),
则直线l与y=F(x)的图象有两个切点即为直线l与
y1=--lnx,x∈(s,t)和
y2=+lnx,x∈(t,+∞)的切点.
y
1'=
-
=
,y
2'=-
+
=
,
设切点分别为A(x
1,y
1),B(x
2,y
2),则0<x
1<x
2,且
=
=-
-
,
=
=
+
,
=
,
即
=1-lnx
1…①;
=1-lnx
2…②;a=
,③
①-②得:
-
=-lnx
1+lnx
2=-ln
,
由③中的a代入上式可得:(
-
)•
=-ln,
即
=ln,…(14分)
令
=k(0<k<1),则(k
2+1)lnk=2k
2-2,令G(k)=(k
2+1)lnk-2k
2+2,(0<k<1),
因为
G()=1-
>0,
G()=-
<0,
故存在k
0∈(0,1),使得G(k
0)=0,
即存在一条过原点的直线l与y=F(x)的图象有两个切点.…(16分)



 备战中考寒假系列答案
备战中考寒假系列答案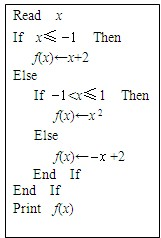 (2013•徐州模拟)已知某算法的伪代码如图,根据伪代码,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是
(2013•徐州模拟)已知某算法的伪代码如图,根据伪代码,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是