数列{an}中,a1=8,a4=2,且满足an+2-2an+1+an=0
(1)求数列的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn.
解:(1)a
n+2-2a
n+1+a
n=0∴a
n+2-a
n+1=a
n+1-a
n∴{a
n+1-a
n}为常数列,
∴{a
n}是以a
1为首项的等差数列,
设a
n=a
1+(n-1)d,a
4=a
1+3d,
∴

,
∴a
n=10-2n.
(2)∵a
n=10-2n,令a
n=0,得n=5.
当n>5时,a
n<0;当n=5时,a
n=0;当n<5时,a
n>0.
∴当n>5时,S
n=|a
1|+|a
2|+…+|a
n|=a
1+a
2+…+a
5-(a
6+a
7+…+a
n)=T
5-(T
n-T
5)=2T
5-T
n,T
n=a
1+a
2+…+a
n.
当n≤5时,S
n=|a
1|+|a
2|+…+|a
n|=a
1+a
2+…+a
n=T
n.
∴
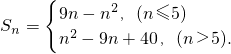
分析:(1)首先判断数列{a
n}为等差数列,由a
1=8,a
4=2求出公差,代入通项公式即得.
(2)首先判断哪几项为非负数,哪些是负数,从而得出当n>5时,S
n=|a
1|+|a
2|+…+|a
n|=a
1+a
2+…+a
5-(a
6+a
7+…+a
n)求出结果;当n≤5时,S
n=|a
1|+|a
2|+…+|a
n|=a
1+a
2+…+a
n当,再利用等差数列的前n项和公式求出答案.
点评:考查了等差数列的通项公式和前n项和公式,求出公差,用代入法直接可求;(2)问的关键是断哪几项为非负数,哪些是负数,属于中档题.

 ,
,