
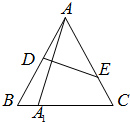 如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,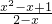 (0≤x≤1),
(0≤x≤1),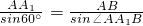 =
=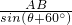 ,
,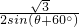
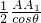 =
=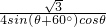 θ∈[0°,60°]
θ∈[0°,60°]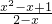 (0≤x≤1),
(0≤x≤1), =
=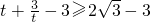
 时,即x=2-
时,即x=2- 时等号成立,AD长度的最小值为2
时等号成立,AD长度的最小值为2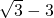 .
.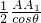 =
=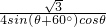
 cos2θ=sin2θ+
cos2θ=sin2θ+ (1+cos2θ)=2sin(2θ+60°)+
(1+cos2θ)=2sin(2θ+60°)+ .
.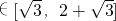 ,∴AD
,∴AD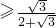 =
= (2-
(2- ),
),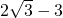 ,当且仅当
,当且仅当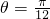 时取最小值.
时取最小值.

科目:高中数学 来源: 题型:
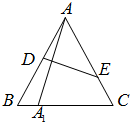 如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,查看答案和解析>>
科目:高中数学 来源: 题型:044
如图,在边长为1的等边△ABC中。圆O1为△ABC的内切圆。圆O2与圆O1外切,且与AB、BC相切……圆On-1,与圆On外切,且与AB、BC相切,如此无限继续下去,记圆On的面积为an(n∈N)。
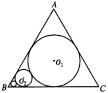
(1)证明:{an}是等比数列;
(2)求![]() (a1+a2+a3+…+an)的值。
(a1+a2+a3+…+an)的值。
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高一3月月考数学试卷(解析版) 题型:解答题
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
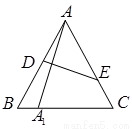
(1)①设A1B=x,用x表示AD;②设∠A1AB=θ∈[0º,60º],用θ表示AD
(2)求AD长度的最小值.
查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试文科数学(广东卷解析版) 题型:解答题
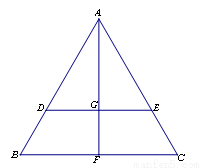
如图,在边长为1的等边三角形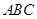 中,
中,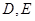 分别是
分别是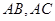 边上的点,
边上的点,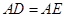 ,
,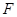 是
是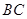 的中点,
的中点,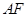 与
与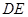 交于点
交于点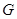 ,将
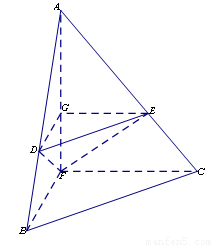
,将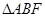 沿
沿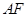 折起,得到如图所示的三棱锥
折起,得到如图所示的三棱锥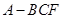 ,其中
,其中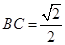 .
.
(1) 证明: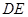 //平面
//平面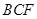 ;
;
(2) 证明: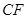
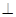 平面
平面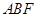 ;
;
(3) 当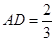 时,求三棱锥
时,求三棱锥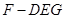 的体积
的体积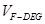 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com