
(1) 已知曲线C :
: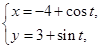 (t为参数), C
(t为参数), C :
: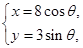 (
(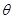 为参数)。化C
为参数)。化C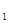 ,C
,C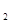 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)求两个圆ρ=4cosθ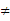 0, ρ=4sinθ的圆心之间的距离,并判定两圆的位置关系。
0, ρ=4sinθ的圆心之间的距离,并判定两圆的位置关系。
科目:高中数学 来源: 题型:
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 36 |
| 4cos2θ+9sin2θ |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 4 |
| 1 |
| 9 |
| (a+b+c)2 |
| 14 |
查看答案和解析>>
科目:高中数学 来源:2011届新疆农七师高级中学高三第一次模拟考试数学理卷 题型:解答题
(共12分)(考生在下面两题中任选一题解答,若多选则安所做的第一题计分)
选修4—4:坐标系与参数方程
1:已知曲线C的极坐标方程是 ,设直线
,设直线 的参数方程是
的参数方程是 (
( 为参数)。
为参数)。
(1)将曲线C的极坐标方程转化为直角坐标方程;
(2)设直线 与
与 轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年新疆农七师高级中学高三第一次模拟考试数学理卷 题型:解答题
(共12分)(考生在下面两题中任选一题解答,若多选则安所做的第一题计分)
选修4—4:坐标系与参数方程
1:已知曲线C的极坐标方程是 ,设直线
,设直线 的参数方程是
的参数方程是 (
( 为参数)。
为参数)。
(1)将曲线C的极坐标方程转化为直角坐标方程;
(2)设直线 与
与 轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com