
已知函数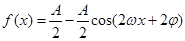
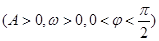 ,且
,且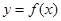 的最大值为2,其图象相邻两对称轴间的距离为2,并过点
的最大值为2,其图象相邻两对称轴间的距离为2,并过点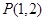 .
.
(1)求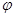 的值;
的值;
(2)若函数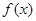 在
在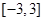 上的图象与
上的图象与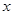 轴的交点分别为
轴的交点分别为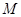 、
、 ,求
,求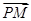 与
与 的夹角.
的夹角.
(1)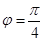 .
(2)即
.
(2)即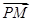 与
与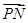 的夹角为
的夹角为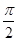 .
.
【解析】本试题主要是考查了三角函数图像的性质以及三角函数解析式的求解,以及运用图像与图像的交点问题,解决点的坐标,进而求解向量的数量积问题的综合运用。
(1)根据三角函数中相邻对称轴之间的距离即为半个周期求解得到w的值,以及最值得到A的值,然后代点得到参数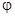 的值。
的值。
(2)根据第一问,利用三角函数与x轴的交点得到M,N的坐标,然后表示向量的数量积,得到夹角公式。
(1)由题可知,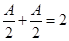 ,即
,即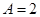 ;
; 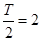 ,即
,即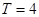 ,
,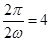 ,
,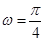 .
.
∴ 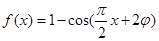 , 又其图象过点
, 又其图象过点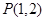 ,
,
∴ 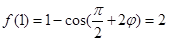 ,即
,即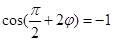 ,
,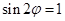 ,
,
∴ 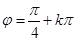 (
(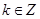 ),而
),而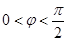 ,故
,故 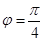 .
…… 6分
.
…… 6分
(2)由(1)可知,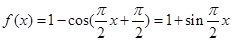 ,
,
∴ 由函数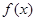 的图象易知,
的图象易知,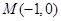 ,
,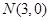 , 又
, 又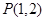 ,故
,故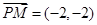 ,
,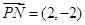 . ∴
. ∴ 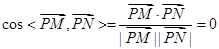 ,即
,即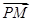 与
与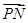 的夹角为
的夹角为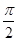


科目:高中数学 来源:2014届江西省高三年级联考文科数学试卷(解析版) 题型:解答题
已知函数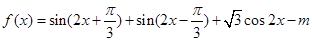 ,若
,若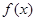 的最大值为1.
的最大值为1.
(1)求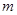 的值,并求
的值,并求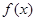 的单调递增区间;
的单调递增区间;
(2)在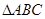 中,角
中,角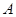 、
、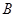 、
、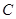 的对边
的对边 、
、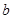 、
、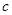 ,若
,若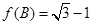 ,且
,且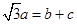 ,试判断三角形的形状.
,试判断三角形的形状.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三第三次月考考试文科数学 题型:选择题
已知函数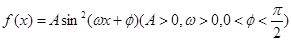 ,且
,且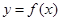 的最大值为2,其图像相邻两对称轴间的距离为2,并过点(1,2).则
的最大值为2,其图像相邻两对称轴间的距离为2,并过点(1,2).则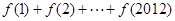 =( )
=( )
A. 0 B. 1 C. 2011 D. 2012
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省台州市高三调研考试理数 题型:解答题
(本题满分14分)
已知函数 .
.
(Ⅰ)求 的最大值及取得最大值时的
的最大值及取得最大值时的 集合;
集合;
(Ⅱ)设 的角
的角 的对边分别为
的对边分别为 ,且
,且 .求
.求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com