
【题目】设![]() ,已知函数
,已知函数 与函数
与函数![]() 有交点,且交点横坐标之和不大于
有交点,且交点横坐标之和不大于![]() ,求
,求![]() 的取值范围_________。
的取值范围_________。
【答案】![]() .
.
【解析】
将原问题进行等价转化,然后结合函数的解析式分类讨论即可确定![]() 的取值范围.
的取值范围.
原问题等价于:设![]() ,已知函数
,已知函数 ,且所有零点之和不大于
,且所有零点之和不大于![]() ,求
,求![]() 的取值范围.分类讨论:
的取值范围.分类讨论:
(1)a<0时,当x≤0时,![]() ,
,![]() ,故
,故![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,所以
,所以![]() 在
在![]() 上有一个零点
上有一个零点![]() ,
,
当![]() 时,
时,![]() ,其对称轴为
,其对称轴为![]() ,
,
则![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,
则![]() 在
在![]() 上有一个零点
上有一个零点![]() ,
,
![]() ,所以符合题意.
,所以符合题意.
(2)当![]() 时,
时,
①![]() 时,当
时,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,所以
,所以![]() 在
在![]() 上没有零点,
上没有零点,
当![]() 时,
时,![]() ,
,![]() .
.
则![]() 在
在![]() 上没有零点,不符合题意;
上没有零点,不符合题意;
②![]() 时,当
时,当![]() 时,
时,![]() ,
,
令![]() 可得
可得![]() ,
,
又![]() 时,
时,![]() 单调递减;
单调递减;
![]() 时,
时,![]() 单调递增,
单调递增,
又![]() ,
,
则![]() 在
在![]() 上有极小值
上有极小值![]() ,
,
所以![]() 在
在![]() 上没有零点,
上没有零点,
当![]() 时,
时,![]() ,
,![]() ,
,
则![]() 在
在![]() 上没有零点,不符合题意;
上没有零点,不符合题意;
③![]() 时,
时, .
.
当![]() 时,
时,![]() ,令
,令![]() 得
得![]() ,
,
又![]() 时,
时,![]() 单调递减;
单调递减;
![]() 时,
时,![]() 单调递增,
单调递增,
则![]() 在
在![]() 上有极小值
上有极小值![]() ,
,
则![]() 在
在![]() 上没有零点,
上没有零点,
![]() 在
在![]() 上有一个零点为
上有一个零点为![]() ,满足题意;
,满足题意;
④a>4时,
当![]() 时,
时,![]() ,令
,令![]() 可得
可得![]() ,
,
又![]() 时,
时,![]() 单调递减;
单调递减;
![]() 时,
时,![]() 单调递增,
单调递增,
且![]() ,
,
则![]() 在
在![]() 上有极小值
上有极小值![]() ,
,
则![]() 在
在![]() 上没有零点,
上没有零点,
![]() 时,
时,![]() ,其对称轴
,其对称轴![]() ,
,
![]() ,且
,且![]() ,
,
根据韦达定理可判断![]() 在
在![]() 上有两个零点,且两根之和为
上有两个零点,且两根之和为![]() ,所以
,所以![]() 时符合题意.
时符合题意.
综上,![]() 的取值范围为
的取值范围为![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】教育学家分析发现加强语文阅读理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲乙两个同类班级进行试验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面的![]() 列联表(单位:人)
列联表(单位:人)
优秀人数 | 非优秀人数 | 总计 | |
甲班 |
|
|
|
乙班 |
|
|
|
总计 |
|
|
|
(1)能否据此判断有![]() 把握认为加强语文阅读训练与提高数学应用题得分率有关?
把握认为加强语文阅读训练与提高数学应用题得分率有关?
(2)经过多次测试后,小明正确解答一道数学应用题所用的时间在![]() 分钟,小刚正确解答一道数学应用题所用的时间在
分钟,小刚正确解答一道数学应用题所用的时间在![]() 分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
(3)现从乙班成绩优秀的![]() 名同学中任意抽取两人,并对他们的答题情况进行全程研究,记
名同学中任意抽取两人,并对他们的答题情况进行全程研究,记![]() 两人中被抽到的人数为
两人中被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
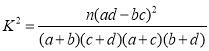
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知偶函数![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .关于偶函数
.关于偶函数![]() 的图象
的图象![]() 和直线
和直线![]() 的
的![]() 个命题如下:
个命题如下:
①当![]() 时,存在直线
时,存在直线![]() 与图象
与图象![]() 恰有
恰有![]() 个公共点;
个公共点;
②若对于![]() ,直线
,直线![]() 与图象
与图象![]() 的公共点不超过
的公共点不超过![]() 个,则
个,则![]() ;
;
③![]() ,
,![]() ,使得直线
,使得直线![]() 与图象
与图象![]() 交于
交于![]() 个点,且相邻点之间的距离相等.
个点,且相邻点之间的距离相等.
其中正确命题的序号是( ).
A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 |
| |
乙班 |
| 30 | |
总计 |
|
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 列联表中![]() 的值为30,
的值为30,![]() 的值为35
的值为35
B. 列联表中![]() 的值为15,
的值为15,![]() 的值为50
的值为50
C. 根据列联表中的数据,若按![]() 的可靠性要求,能认为“成绩与班级有关系”
的可靠性要求,能认为“成绩与班级有关系”
D. 根据列联表中的数据,若按![]() 的可靠性要求,不能认为“成绩与班级有关系”
的可靠性要求,不能认为“成绩与班级有关系”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 坐标为
坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() .记过
.记过![]() 、
、![]() 、
、![]() 三点的圆为圆
三点的圆为圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求过点![]() 与圆
与圆![]() 相交所得弦长为
相交所得弦长为![]() 的直线方程.
的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的圆心为
的圆心为![]() .已知点
.已知点![]() ,且
,且![]() 为圆
为圆![]() 上的动点,线段
上的动点,线段![]() 的中垂线交
的中垂线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,若四边形
,若四边形![]() 的四个顶点都在曲线
的四个顶点都在曲线![]() 上,对角线
上,对角线![]() ,
,![]() 互相垂直并且它们的交点恰为点
互相垂直并且它们的交点恰为点![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是腾讯开发的一个记录跑步或行走情况(步数里程)的公众号用户通过该公众号可查看自己某时间段的运动情况.某人根据2018年1月至2018年11月期间每月离步的里程(单位:十公里)的数据绘制了下面的折线图.根据该折线图,下列结论正确的是( )

A.月跑步里程逐月增加
B.月跑步里程最大值出现在10月
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com