
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,椭圆
,椭圆![]() 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]()
![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() (0,1),且
(0,1),且![]() =
=![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)由椭圆![]() 上任意一点到椭圆两个焦点的距离之和为
上任意一点到椭圆两个焦点的距离之和为![]() 可得
可得![]() ,由
,由![]() 的焦距为
的焦距为![]() ,可得
,可得![]() ,再由
,再由![]() 的关系可得
的关系可得![]() ,进而得到椭圆方程;(II)直线
,进而得到椭圆方程;(II)直线![]() 代入椭圆方程,运用韦达定理和判别式大于
代入椭圆方程,运用韦达定理和判别式大于![]() ,再由中点坐标公式和两直线垂直的条件,可得
,再由中点坐标公式和两直线垂直的条件,可得![]() 的方程,解方程可得
的方程,解方程可得![]() ,从而可得直线方程.
,从而可得直线方程.
试题解析:(Ⅰ)由已知![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,
,
所以![]() ,
,
所以椭圆C的方程为![]() 。
。
(Ⅱ)由 得
得![]() ,
,
直线与椭圆有两个不同的交点,所以![]() 解得
解得![]() 。
。
设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() )
)
则![]() ,
,![]() ,
,
计算![]() ,
,
所以,A,B中点坐标E(![]() ,
,![]() ),
),
因为![]() =
=![]() ,所以PE⊥AB,
,所以PE⊥AB,![]() ,
,
所以 , 解得
, 解得![]() ,
,
经检验,符合题意,所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】从某企业的某种产品中抽取![]() 件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
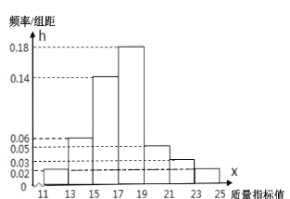
(Ⅰ)求这![]() 件产品质量指标值的样本平均数
件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表,记作
(同一组数据用该区间的中点值作代表,记作![]() ,
,![]() );
);
(Ⅱ)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)若使![]() 的产品的质量指标值高于企业制定的合格标准,则合格标准的质量指标值大约为多少?
的产品的质量指标值高于企业制定的合格标准,则合格标准的质量指标值大约为多少?
(ii)若该企业又生产了这种产品![]() 件,且每件产品相互独立,则这
件,且每件产品相互独立,则这![]() 件产品质量指标值不低于
件产品质量指标值不低于![]() 的件数最有可能是多少?
的件数最有可能是多少?
附:参考数据与公式:![]() ,
,![]() ;若
;若![]() ,则①
,则①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{![]() }的首项a1=2,前n项和为
}的首项a1=2,前n项和为![]() ,且数列{
,且数列{![]() }是以
}是以![]() 为公差的等差数列·
为公差的等差数列·
(1)求数列{![]() }的通项公式;
}的通项公式;
(2)设![]() ,
,![]() ,数列{
,数列{![]() }的前n项和为
}的前n项和为![]() ,
,
①求证:数列{![]() }为等比数列,
}为等比数列,
②若存在整数m,n(m>n>1),使得![]() ,其中
,其中![]() 为常数,且
为常数,且![]() -2,求
-2,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,且∠AOC=120°,PA⊥平面ABC,AB=4,PA=2![]() ,D是PC的中点,点M是⊙O上的动点(不与A,C重合).
,D是PC的中点,点M是⊙O上的动点(不与A,C重合).

(1)证明:AD⊥PB;
(2)当三棱锥D﹣ACM体积最大时,求面MAD与面MCD所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:![]() ):男生成绩在175
):男生成绩在175![]() 以上(包括175
以上(包括175![]() )定义为“合格”,成绩在175
)定义为“合格”,成绩在175![]() 以下(不包括175
以下(不包括175![]() )定义为“不合格”.女生成绩在165
)定义为“不合格”.女生成绩在165![]() 以上(包括165
以上(包括165![]() )定义为“合格”,成绩在165
)定义为“合格”,成绩在165![]() 以下(不包括165
以下(不包括165![]() )定义为“不合格”.
)定义为“不合格”.

(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用![]() 表示其中男生的人数,写出
表示其中男生的人数,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数![]() ,将满足“
,将满足“![]() 且
且![]() 为整数”的实数
为整数”的实数![]() 称为实数
称为实数![]() 的小数部分,用记号
的小数部分,用记号![]() 表示.对于实数
表示.对于实数![]() ,无穷数列
,无穷数列![]() 满足如下条件:
满足如下条件:![]() ,
, 其中
其中![]() .
.
(1)若![]() ,求数列
,求数列![]() ;
;
(2)当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() ,求符合要求的实数
,求符合要求的实数![]() 构成的集合
构成的集合![]() ;
;
(3)若![]() 是有理数,设
是有理数,设![]() (
(![]() 是整数,
是整数,![]() 是正整数,
是正整数,![]() 互质),问对于大于
互质),问对于大于![]() 的任意正整数
的任意正整数![]() ,是否都有
,是否都有![]() 成立,并证明你的结论.
成立,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com