练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知O是△ABC内一点，且满足
    OA
    •
    OB
    =
    OB
    •
    OC
    =
    OC
    •
    OA
    ，则O点一定是△ABC的（　　）
    分析：利用
    OA
    •
    OB
    =
    OB
    •
    OC
    =
    OC
    •
    OA
    ，由平面向量的运算法则，能推导出
    OB
    ⊥
    CA
    ，
    OA
    ⊥
    CB
    ，
    OC
    ⊥
    AB
    ，由此能求出结果．
    解答：解：O是△ABC内一点，且满足
    OA
    •
    OB
    =
    OB
    •
    OC
    =
    OC
    •
    OA
    ，
    ∴
    OA
    •
    OB
    -
    OB
    •
    OC
    =0，
    ∴
    OB
    •(
    OA
    -
    OC
    )    =
    OB
    •
    CA
    =0，
    ∴
    OB
    ⊥
    CA
    ，
    ∵
    OA
    •
    OB
    -
    OC
    •
    OA
    =0，
    ∴
    OA
    •(
    OB
    -
    OC
    )=
    OA
    •
    CB
    =0    ，
    ∴
    OA
    ⊥
    CB
    ，
    ∵
    OB
    •
    OC
    -
    OC
    •
    OA
    =0，
    ∴
    OC
    •(
    OB
    -
    OA
    )    =
    OC
    •
    AB
    =0，
    ∴
    OC
    ⊥
    AB
    ，
    ∴O点一定是△ABC的垂心．
    故选C．
    点评：本题考查平面向量的应用，解题时要注意平面运算法则的灵活运用，是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知O为平面内一定点，设条件p：动点M满足
    OM
    =
    OA
    +λ（
    AB
    +
    AC
    ），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（　　）
    A、充要条件
    B、充分不必要条件
    C、必要不充分条件
    D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知O是△ABC所在平面内的一定点，动点P满足
    OP
    =
    OA
    +λ(
    AB
    |
    AB
    |
    +
    AC
    |
    AC
    |
    )    ，λ∈（0，+∞），则动点P的轨迹一定通过△ABC的（　　）

    查看答案和解析>>

    科目：高中数学 来源：高中数学全解题库(国标苏教版·必修4、必修5) 苏教版 题型：013

    已知O是△ABC内一点，存在一组正实数λl，λ2，λ3，使，则∠AOB，∠BOC，∠COA

    [　　]

    A．都是钝角

    B．至多有两个钝角

    C．恰有两个钝角

    D．至少有两个钝角

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知O为平面内一定点，设条件p：动点M满足
    OM
    =
    OA
    +λ（
    AB
    +
    AC
    ），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（　　）
    A．充要条件B．充分不必要条件
    C．必要不充分条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年陕西省宝鸡中学高三（上）第一次月考数学试卷（理科）（解析版） 题型：选择题

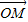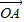    已知O为平面内一定点，设条件p：动点M满足=+λ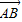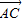（+），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（ ）
    A．充要条件
    B．充分不必要条件
    C．必要不充分条件
    D．既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案